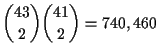The purpose of this file is to investigate the probabilities of bad beat
jackpots occurring in Omaha under a variety of qualifying conditions.
There are a large number of conditions imposed by different cardrooms so
we do not intend to exhaust all possible situations. We shall try to
cover some of the common situations.
We are interested in the probability that a bad beat jackpot will occur
but not the probability that particular players will be involved. Thus,
we are interested in semi-deals. The first number we need is the total
number of semi-deals possible in a 10-handed Omaha game. The number
of possible boards is
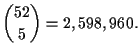 |
|
|
(1) |
There are then
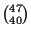 ways to choose the 40 cards to be dealt
to the players. Since we are counting semi-deals, we need to know how many
partitions of a 40-set into 10 sets of 4 elements each there are. We keep
choosing 4 elements at a time and divide by 10! at the end because the
same partition could be chosen in any of 10! orders. Hence, there are
ways to choose the 40 cards to be dealt
to the players. Since we are counting semi-deals, we need to know how many
partitions of a 40-set into 10 sets of 4 elements each there are. We keep
choosing 4 elements at a time and divide by 10! at the end because the
same partition could be chosen in any of 10! orders. Hence, there are
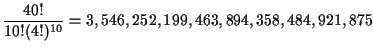 |
|
|
(2) |
semi-deals for a fixed set of 40 cards to 10 players with
each player receiving 4 cards. We take the product of (1), (2) and
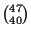 to get
to get
| 579,643,753,025,138,828,150,090,204,093,424,318,750,000 |
|
|
(3) |
total possible semi-deals for 10-handed Omaha.
For the next step we want to extend part of the preceding calculation
in order to get some useful numbers. If 36 cards are being distributed
to 9 players in hands of 4 cards each, then the number of possible
semi-deals is
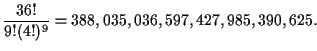 |
|
|
(4) |
Similarly, if 32 cards are being distributed to 8 players, then there
are
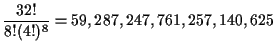 |
|
|
(5) |
semi-deals. Continuing, if 28 cards are being distributed
to 7 players, then there are
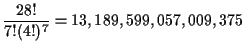 |
|
|
(6) |
semi-deals. Finally, if 24 cards are being distributed
to 6 players, the number of semi-deals is
We are going to impose the condition that a player holding 4-of-a-kind
must have a pair in her hand in order for the hand to qualify for a bad
beat jackpot. We now examine the probability that 2 players end up
with 4-of-a-kind. In order for this to occur, the board must have rank
multiset
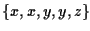 because of the condition we imposed. There are
123,552 such boards (see the file entitled 5-Card Poker Hands). For a
given board with two pairs in it, 2 players will end up with 4-of-a-kind
provided that the remaining 2 cards of rank x are dealt to some player
and the remaining 2 cards of rank y are dealt to another player. Thus,
in forming semi-deals which qualify, we are choosing 2 cards from 43 to
join the 2 cards of rank x for 1 hand, and we are choosing another 2
cards from the remaining 41 to join the 2 cards of rank y to form a
second qualifying hand. This can be done in
because of the condition we imposed. There are
123,552 such boards (see the file entitled 5-Card Poker Hands). For a
given board with two pairs in it, 2 players will end up with 4-of-a-kind
provided that the remaining 2 cards of rank x are dealt to some player
and the remaining 2 cards of rank y are dealt to another player. Thus,
in forming semi-deals which qualify, we are choosing 2 cards from 43 to
join the 2 cards of rank x for 1 hand, and we are choosing another 2
cards from the remaining 41 to join the 2 cards of rank y to form a
second qualifying hand. This can be done in
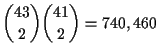 |
|
|
(8) |
ways and it counts the number of ways we can form 2 hands
producing 2 4-of-a-kind hands with a fixed board having rank multiset
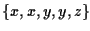 .
For the other 8 players, we choose 32 cards from the
39 cards left over. They can be partitioned into the number of semi-deals
shown in (5) above. Thus, if we take the product of (5), (8), 123,552
and
.
For the other 8 players, we choose 32 cards from the
39 cards left over. They can be partitioned into the number of semi-deals
shown in (5) above. Thus, if we take the product of (5), (8), 123,552
and
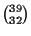 ,
we obtain the total number of semi-deals producing
2 players with qualifying 4-of-a-kind hands. Dividing by (3) then gives
the probability of this happening. Doing all this arithmetic produces a
probability of .0001439243598 for 4-of-a-kind losing to another 4-of-a-kind,
where each of the players has a pair in her hand matching a pair on board.
This number is about 1 in 7,000 which is considerably bigger than any of
the hold'em bad beat jackpot probabilities, and we have not yet considered
the effect of straight flushes beating 4-of-a-kind which will increase
the likelihood of quads losing. Hence, we certainly shall not go with
a lower threshold than quads losing.
,
we obtain the total number of semi-deals producing
2 players with qualifying 4-of-a-kind hands. Dividing by (3) then gives
the probability of this happening. Doing all this arithmetic produces a
probability of .0001439243598 for 4-of-a-kind losing to another 4-of-a-kind,
where each of the players has a pair in her hand matching a pair on board.
This number is about 1 in 7,000 which is considerably bigger than any of
the hold'em bad beat jackpot probabilities, and we have not yet considered
the effect of straight flushes beating 4-of-a-kind which will increase
the likelihood of quads losing. Hence, we certainly shall not go with
a lower threshold than quads losing.
Brian &
2000-11-02
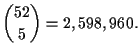
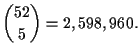
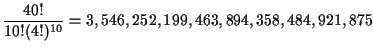
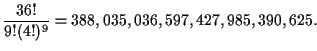
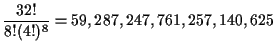
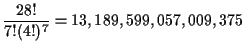
![]() because of the condition we imposed. There are
123,552 such boards (see the file entitled 5-Card Poker Hands). For a
given board with two pairs in it, 2 players will end up with 4-of-a-kind
provided that the remaining 2 cards of rank x are dealt to some player
and the remaining 2 cards of rank y are dealt to another player. Thus,
in forming semi-deals which qualify, we are choosing 2 cards from 43 to
join the 2 cards of rank x for 1 hand, and we are choosing another 2
cards from the remaining 41 to join the 2 cards of rank y to form a
second qualifying hand. This can be done in
because of the condition we imposed. There are
123,552 such boards (see the file entitled 5-Card Poker Hands). For a
given board with two pairs in it, 2 players will end up with 4-of-a-kind
provided that the remaining 2 cards of rank x are dealt to some player
and the remaining 2 cards of rank y are dealt to another player. Thus,
in forming semi-deals which qualify, we are choosing 2 cards from 43 to
join the 2 cards of rank x for 1 hand, and we are choosing another 2
cards from the remaining 41 to join the 2 cards of rank y to form a
second qualifying hand. This can be done in