Threshold Quads

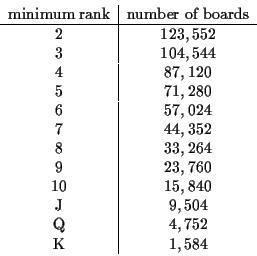
Now we shall examine what happens as we increase the rank of qualifying quads. The first step is to count the number of boards with rank multiset $\{x,x,y,y,z\}$ as we increase the minimum rank of the pair. Above we observed that there are 123,552 boards with rank multiset of that form. If, for example, we insist the smallest rank of the pairs is at least 3, then x,y are being chosen from a 12-set. So there are 66 choices for the ranks of the pairs, 6 choices for each of the pairs, and 44 choices for the fifth card. This gives us 104,544 boards with this additional restriction. The next table gives the number of boards with rank multiset $\{x,x,y,y,z\}$ as the minimum rank of the pairs varies.

$$\begin{array}{c\vert c} \mbox{minimum rank} & \mbox{number of... ... 9,504\\ {\mathrm Q} & 4,752\\ {\mathrm K} & 1,584 \end{array}$$

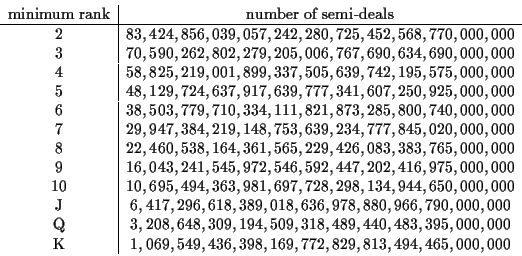
In the introductory section, we saw that the number of qualifying semi-deals for 2 players having 4-of-a-kind is obtained by taking the product of (5), (8), ${{39}\choose{32}}$ and 123,552. In order to get the number of qualifying semi-deals as we change the threshold of which 4-of-a-kind hands qualify, we take the same product except we replace 123,552 with the appropriate entry from the table above. Upon doing so we get the next table which then may be used to determine the probability that 2 players will have qualifying 4-of-a-kind hands, where the minimum qualifying hand is quads of a certain rank. For example, if the minimum qualifying hand is quad sixes, then look at the entry for number of semi-deals in the row corresponding to minimum rank 6 in the next table and divide by (3) to get the probability.

$$\begin{array}{c\vert c} \mbox{minimum rank} & \mbox{number of... ...& 1,069,549,436,398,169,772,829,813,494,465,000,000 \end{array}$$