Just above we determined the probability of a semi-deal occurring in Omaha for which 2 players have straight flushes and saw that it is roughly 1 in 36,000. Now we want to determine the probability that 4-of-a-kind or better loses with varying minimum ranks of the quads being required. In the preceding sections, we have counted the number of semi-deals for which either 2 players have 4-of-a-kind or 2 players have straight flushes. However, those 2 counts overlap, that is, there are some semi-deals for which 2 people will have qualifying straight flushes and 2 people will make 4-of-a-kind (the sets of 2 people may overlap, that is, 1 person could have both quads and a straight flush)We want to eliminate all double counting.
The board must have a rank multiset of the form
![]() in order
for 2 players to have 4-of-a-kind. On the other hand, in order for 2
players to have straight flushes, the ranks must be successive, that is,
of the form w,w+1,w+2. We are going to count the number of boards
of this form with a varying restriction on the minimum rank of the pair.
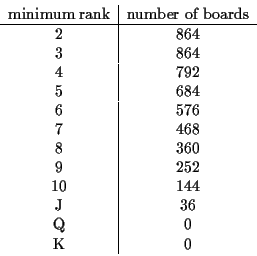
If there is no restriction on the rank, there are 4 choices for suit, 3
choices for which of the 2 ranks will be paired, 3 choices for each of
the pairing cards not in the flush suit, and 8 choices for w. Altogether
we have 864 such boards. Note that the smallest rank which can occur is
3 (in order to allow a straight flush at the bottom). If we insist quads
must have rank at least 4, then when x=3, we have no choice for the 2
ranks being paired so that we lose 1/12
th of the boards.
Thus, there are 792 boards. Continuing in this vein, we get the
following table for the number of possible boards.
in order
for 2 players to have 4-of-a-kind. On the other hand, in order for 2
players to have straight flushes, the ranks must be successive, that is,
of the form w,w+1,w+2. We are going to count the number of boards
of this form with a varying restriction on the minimum rank of the pair.
If there is no restriction on the rank, there are 4 choices for suit, 3
choices for which of the 2 ranks will be paired, 3 choices for each of
the pairing cards not in the flush suit, and 8 choices for w. Altogether
we have 864 such boards. Note that the smallest rank which can occur is
3 (in order to allow a straight flush at the bottom). If we insist quads
must have rank at least 4, then when x=3, we have no choice for the 2
ranks being paired so that we lose 1/12
th of the boards.
Thus, there are 792 boards. Continuing in this vein, we get the
following table for the number of possible boards.
For a fixed board, there are 8 cards which are determined in order to
give us 2 sets of quads and 2 straight flushes. There several ways in
these cards can go into hands. First, as unlikely as it is, there may
be only 2 players sharing in this bounty. The 2 sets of 2 cards which
produce quads must go to separate players. Then there are 2 ways the
straight flush cards can be distributed to the same player. There are
then 32 cards to be chosen from the remaining 39 cards to be distributed
to the remaining 8 players. Thus, we take the product of 2, (5) and
![]() to get the number of semi-deals with exactly 2
players making the big hands. This produces
to get the number of semi-deals with exactly 2
players making the big hands. This produces
| 1,823,786,845,438,574,241,506,531,250 | (13) |
Another possibility is that 3 players share the 8 big cards. The 2
sets of cards making quads must go to 2 different hands. Now there
are 2 choices for which 2 straight flush cards are going to join a
hand making quads, and there are 2 choices for which hand to put it
with. This gives us 4 combinations with 3 players sharing the big
cards. We now choose 2 cards from 39 to go with 1 hand, 2 cards from
37 to go with the other hand, and 28 from 35 to be distributed to the
remaining 7 players. The product of all these numbers and (6) is taken
to produce
| 175,083,537,162,103,127,184,627,000,000 | (14) |
Finally, if the big cards are spread over 4 players, we choose 2 cards
from 39, 2 from 37, 2 from 35, and 2 from 33 to complete the 4 sets of
cards to Omaha hands. We then choose 24 cards from 31 and distribute
in (7) ways to the remaining 6 players. The product of all the
appropriate numbers gives
| 1,838,377,140,202,082,835,438,583,500,000 | (15) |
The sum of (13), (14) and (15) is the number of semi-deals for each
fixed board which are counted as 2 sets of quads occurring and 2 straight
flushes occurring. This sum is
| 2,015,284,464,209,624,536,864,717,031,250 | (16) |
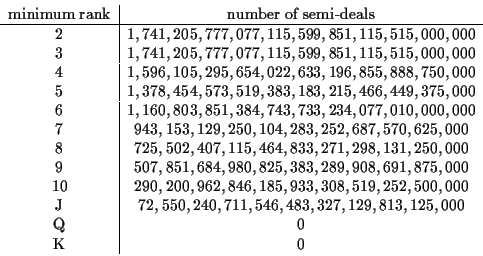
From the preceding table, we see how many semi-deals which have been counted twice. So we now make the final adjustment for these semi-deals. Since (12) counts the number of semi-deals for which 2 players have straight flushes and the second table in Section 2 counts the number of semi-deals for which 2 players get quads with varying threshold ranks, by subtracting the various lines of the preceding table from the sum of (12) and the entries of the table in Section 2, we get the number of semi-deals for which at least 2 players get straight flushes or 2 players get 4-of-a-kind both of some rank or better. This information is contained in the following table.
