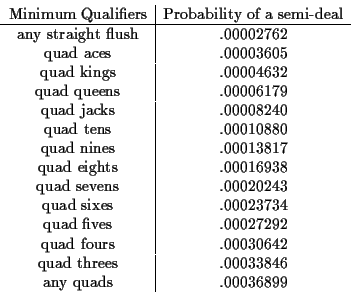
If there are 5 suited cards in the board, then no one can make 4-of-a-kind. Thus, we have taken care of all the possibilities. So now we add all the appropriate entries from various tables to get the number of semi-deals which qualify for a bad beat jackpot in Omaha with a restriction on the minimum qualifying hand. We also have assumed that in the case of 4-of-a-kind, the player must have a pair in her hand in order for the hand to qualify. We then divide by (3) to get the probabilities. The following table presents these final probabilities.
