All graphs in this paper have neither loops nor multiple edges. We use
V(X) and E(X) to denote the vertex set and edge set of X, respectively.
Given a graph X, the complement of X, denoted Xc, satisfies uis adjacent to v in X if and only if u is not adjacent to v in
Xc.
Definition 1.1
A graph X is said to be self-complementary if it is isomorphic
to its complement.
The following proposition is simple to prove so we omit its proof.
Proposition 1.2
Whenever
X is a self-complementary regular graph, we have
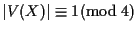
.
Definition 1.3
Let
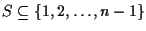 such that
such that 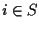 if and only if
if and only if
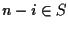 . The
. The
circulant
graph X=
X(
n;
S)
of order n is the graph whose vertex set
is
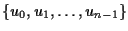 with an edge joining ui and uj if and
only if
with an edge joining ui and uj if and
only if 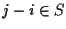 , where the latter computation is done modulo n. The set
S is called the
, where the latter computation is done modulo n. The set
S is called the connection set
of the circulant.
H. Sachs [2] showed how to construct self-complementary circulant
graphs of order n whenever n is a product of primes all of which are
congruent to 1 modulo 4. He further wrote that there are reasons to
conjecture that it is necessary that all
the primes in the prime factorization of n be congruent to 1 modulo 4.
He supported this statement by demonstrating the non-existence of
self-complementary circulant graphs of orders n=p2e, n=pq and
n=9r, where p and q are any primes congruent to 3 modulo 4, and
r>5 is a prime congruent to 1 modulo 4.
D. Froncek, A. Rosa and J. Siran [1] have proved that
his conjecture
is true, that is, they showed that there exists a self-complementary
circulant graph of order n if and only if every prime in the prime
factorization of n is congruent to 1 modulo 4. Their proof is graph
theoretic. In this paper, we provide a simple algebraic proof. First,
some preliminary results about permutation groups are required.
Definition 1.5
Let G be a permutation group acting on 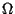 . If
. If
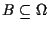 has the property that for every
has the property that for every 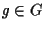 , either
g
, either
g(
B)=
B or
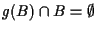 , then B is called a
, then B is called a block
of
G.
It is easy to see that 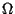 ,
,
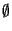 ,
and any singleton are blocks
of any permutation group. They are called trivial blocks for this reason.
All other blocks are called non-trivial.
,
and any singleton are blocks
of any permutation group. They are called trivial blocks for this reason.
All other blocks are called non-trivial.
Definition 1.6
Let G be a transitive permutation group. If G has any non-trivial
blocks, then G is said to be an imprimitive group. Otherwise, Gis said to be primitive.
Note that if G is imprimitive, then given a non-trivial block B,
there is a partition of 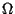 obtained by taking B and all its
images under the action of G. This is called a complete block
system and all the blocks have the same cardinality; the latter is
frequently called the length of a block.
obtained by taking B and all its
images under the action of G. This is called a complete block
system and all the blocks have the same cardinality; the latter is
frequently called the length of a block.
Definition 1.7
Let G be an abstract finite group. If every primitive group containing
the regular representation of G as a transitive subgroup is doubly
transitive, then G is said to be a Burnside group.
Burnside groups are nice groups for graph theory. Why? If we form
any Cayley graph on a Burnside group G, then the regular representation of
G is contained in the automorphism group of the graph as a transitive
subgroup. Hence, if the Cayley graph is neither complete nor the complement
of the complete graph, then the automorphism group must act imprimitively
on the vertex set of the graph. This is especially nice for circulant graphs
because of the following result telling us precisely what the blocks are.
Lemma 1.8
If
n is not prime and the automorphism group
Aut(
X)of a circulant graph
X of order
n acts imprimitively on the vertex set of
X with blocks of
length
d, then
d is a divisor of
n and the blocks are the sets
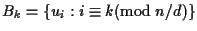
,
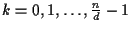
.
PROOF.Let B be a block of length d.
Taking all the blocks belonging to the complete block system containing
B, we see that this partitions the vertex set into parts all of which
have d elements. Thus, d is a divisor of n.
We know that the permutation
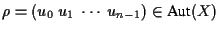 .
By
the definition of blocks and from the action of
.
By
the definition of blocks and from the action of 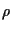 ,
it is easy to see
that each block must be made up of vertices equally spaced n/d apart in
the order in which they occur in
,
it is easy to see
that each block must be made up of vertices equally spaced n/d apart in
the order in which they occur in 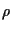 .
This completes the proof.
.
This completes the proof.
The following two known results are required later. The simple proof
of the second is omitted.
Theorem 1.9 ([
3])
The cyclic groups of composite order all are Burnside groups.
Proposition 1.10
Let
G be an imprimitive group with blocks
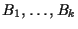
and let
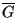
denote the action of
G on the set of blocks. If
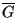
is itself imprimitive with blocks
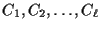
,
then
G is imprimitive with blocks
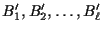
,
where
B'
iis the union of the blocks comprising
Ci.
Brian &
2000-01-24
![]() ,
,
![]() ,
and any singleton are blocks
of any permutation group. They are called trivial blocks for this reason.
All other blocks are called non-trivial.
,
and any singleton are blocks
of any permutation group. They are called trivial blocks for this reason.
All other blocks are called non-trivial.![]() .
By
the definition of blocks and from the action of
.
By
the definition of blocks and from the action of ![]() ,
it is easy to see
that each block must be made up of vertices equally spaced n/d apart in
the order in which they occur in
,
it is easy to see
that each block must be made up of vertices equally spaced n/d apart in
the order in which they occur in ![]() .
This completes the proof.
.
This completes the proof.