Graceful Labeling of Paths with Specified Endpoints
This conjecture comes from Pavol Gvozdjak's Ph.D. thesis. Its solution would have consequences for the Oberwolfach problem. A graceful labeling of a path of length n is a permutation p of the integers {0,1,...,n} such that
{ | p(i) - p(i-1) | : i = 1, 2, ... , n } = {1, 2, ... , n}.
That is, no number appears twice as the absolute difference of consecutive integers in the list p(0), p(1) , ... , p(n). If p(0)=a and p(n)=b, then such a graceful labeling is called an (a, b;i n)-graceful labeling.
Conjecture: An (a, b; n)-graceful labeling exists if and only if the integers a, b, n satisfy,
- b-a has the same parity as 1+2+...+n = n(n+1)/2, and
- 0 < |b-a| <= n/2 <= a+b <= 3n/2.
Comments: The necessity of the first condition is easy to prove, whereas the second is a bit more challenging. The difficulty lies in showing that the conditions are sufficient.
When a or b equals 0 or n, then there is exactly one solution. For example: 0 9 1 8 2 7 3 6 4 5 is the only (0, b ; 9)-graceful labeling for any value of b. When a and b are close to n/2, experiments suggest that there are numerous (a, b; n)-graceful labelings. However we can not yet prove the existence of at least one any solution for each triple a, b,n satisfying the two conditions. Gvozdjak proves in his thesis that there exists at least one (a, b; n)-graceful labeling for each value of a = 0, 1, ... , n. This result also appears (in French) in: E. Flandrin, I. Fournier, A. Germa Numerotations gracieuses des chemins., Ars Combin. 16 (1983), 149--181.
Example: n=15. The following table gives is the number, N(a, b; 15), of (a, b;15)-graceful labelings. Note the four-way symmetry:
N(a, b; n) = N(b, a; n) = N(n-a, n-b; n) = N(n-b, n-a; n).
Computer experiments for n<22 yield similar tables. This table has been shamelessly lifted from Pavol Gvozdjak's thesis.
\ b 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
a \
0 x . . . . . . . 1 . . . . . . .
1 . x . . . . . 56 . 49 . . . . . .
2 . . x . . . 304 . 268 . 157 . . . . .
3 . . . x . 528 . 880 . 852 . 237 . . . .
4 . . . . x . 1270 . 1462 . 1032 . 237 . . .
5 . . . 528 . x . 2136 . 2014 . 1032 . 157 . .
6 . . 304 . 1270 . x . 2734 . 2014 . 852 . 49 .
7 . 56 . 880 . 2136 . x . 2734 . 1462 . 268 . 1
8 1 . 268 . 1462 . 2734 . x . 2136 . 880 . 56 .
9 . 49 . 852 . 2014 . 2734 . x . 1270 . 304 . .
10 . . 157 . 1032 . 2014 . 2136 . x . 528 . . .
11 . . . 237 . 1032 . 1462 . 1270 . x . . . .
12 . . . . 237 . 852 . 880 . 528 . x . . .
13 . . . . . 157 . 268 . 304 . . . x . .
14 . . . . . . 49 . 56 . . . . . x .
15 . . . . . . . 1 . . . . . . . x
Circuit Double Cover Conjecture
P. Seymour (1979) posed the following problem. An equivalent conjecture was stated (with a slight error) by Szekeres (1973).Conjecture: If every edge of a graph G is contained in a circuit (that is, G has no coloops), then there exists a list of circuits such that each of G appears in exactly two circuits in the list.
There are several stronger versions of this conjecture. Here is one of the strongest possible formulations of this conjecture.
Oriented Strong 5-cycle Double Cover Conjecture: If G has no coloops, then G can be embedded on some orientable closed compact surface such that each resulting face can be assigned one of 5 colours, where every edge bounds two faces of different colour. (That is, G has a 5-face colourable strong embedding on an orientable surface,)
Having such an embedding is sort of like saying that the matroidal dual of any graphs, is no more complicated than the set of edge cuts of a complete graph of order 5.
Removable Simple Circuit Conjecture
 This conjecture was independently proposed by myself and Herbert Fleischner.
Fleischner's version is in terms of decompositions of Eulerian graphs having forbidden
transitions at each vertex.
If this conjecture holds true, then it would be a great step toward the
Circuit Double Cover conjecture.
A decomposition of a graph G (multiple edges are allowed)
is a partition of its edge set.
The general question is: Which graphs can be decomposed into circuits of
length at least three?
Two obvious necessary conditions for such the existence of such a decomposition are:
This conjecture was independently proposed by myself and Herbert Fleischner.
Fleischner's version is in terms of decompositions of Eulerian graphs having forbidden
transitions at each vertex.
If this conjecture holds true, then it would be a great step toward the
Circuit Double Cover conjecture.
A decomposition of a graph G (multiple edges are allowed)
is a partition of its edge set.
The general question is: Which graphs can be decomposed into circuits of
length at least three?
Two obvious necessary conditions for such the existence of such a decomposition are:
- Each vertex of G has even degree.
- No 2-connected block of G has fewer than 3 edges.
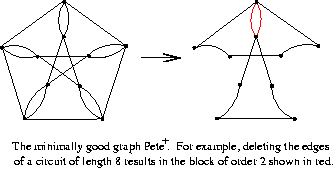
 As illustrated at right, the graph, Pete+, obtained from Petersen's graph
by replacing each edge of a perfect matching by an even number of parallel
edges, is minimally good.
As illustrated at right, the graph, Pete+, obtained from Petersen's graph
by replacing each edge of a perfect matching by an even number of parallel
edges, is minimally good.
Conjecture: The only 3-connected minimally good graph having edge multiplicities at most 2 is Pete+.
It is shown in [AGZ] that if G is a 3-connected minimally good graph with edge multiplicities at most 2, then G is a 4-regular graph obtained from two odd circuits of equal length by adding digons (circuits of length 2), where each digon has one vertex from each circuit of odd length (see diagram).
Thin spanning trees and Jaeger's flow conjecture
If a graph is oriented, then the edge set B of an edge cut (B is a cocircuit) is naturally partitioned (B+, B-) into two (possibly empty) subsets, depending on edge directions. The goal is to find an orientation of G such that the ratio |B+| : |B-| is as close to 1:1 as possible, simultaneously for each cocircuit B.
Conjecture: (Jaeger) If G is 4k-edge connected, then for some orientation of G, every cocircuit B satisfies
This problem has several reformulations and refinements. Jaeger's formulation is in terms of "nice modular p-flows". The conclusion of this conjecture is equivalent to G having circular flow number at most 2 + 1/k. It is also equivalent to G having a real-valued circulation in which all edges get a flow value in the interval [1, 1+1/k]. Jaeger's conjecture has not been proved for any positive integer k. For k=1, this is Tutte's 3-flow conjecture. For planar graphs, the conjecture is proved only for k=1 (Groetzsch's theorem). The situation is no better even if "4k" is replaced by an arbitrary function of k(!!).
Here is an attractive variation. A spanning tree T is e-thin if for every edge cut B, at most e|B| edges in B belong to T.
Conjecture: (Goddyn) There exists a function f such that, for e >0, every f(e)-edge connected graph has an e-thin spanning tree.
Jaeger's conjecture would follow if this were conjecture were true with f(e) = 2/e-2.
Since every 2k-edge connected graph has k pairwise edge disjoint spanning trees, then at least one of these trees is "1/k-thin" relative to any fixed cocircuit B. The problem is to make the same tree thin on every cocircuit B. It is an amusing exercise to prove these conjecture for any natural family of k-edge connected graphs, such as complete graphs and hypercubes.
Accumulated quotients (just for fun)
 This is a number-theoretic problem, which is quite fun, and, actually is not unsolved.
For integers 0 <= s <= m,
let fm(s) denote the integer ns where
This is a number-theoretic problem, which is quite fun, and, actually is not unsolved.
For integers 0 <= s <= m,
let fm(s) denote the integer ns where
n0 = m and ni+1 = ni + floor( ni / s ) for i >= 0.
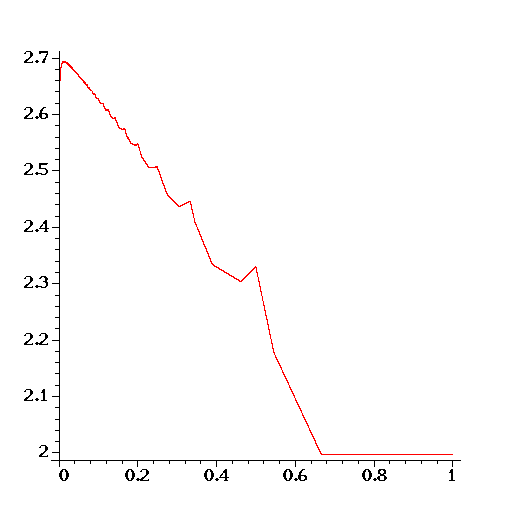
By plotting fm(s) versus s for large values of m it becomes apparent that, after renormalizing, there is a limit function f: (0,1] -> [2,3] defined by
f(x) = lim_{m -> \infty} fm( floor(xm) )/m
Shown at right is an approximate plot of f(x) versus x (obtained by setting m=10000). The challenge is to prove that f(x) exists and to determine the limit function f.