Math 252 Homework Assignment 04
- Due 8:30 AM Friday February 5th, 1999.
- Section 3.1, pages 112-114:
- 5, 8, 10, 12, 17, 21, 23, 29, 32
- Section 3.2, page 117:
- 2
- jh04.1:
- Plot in Maple the isotimic surfaces given by
x^2 + y^2 - z^2 = C^2 for C=1,
C=2, and C=3.
- What is the gradient field of
x^2 + y^2 - z^2 ?
- Plot this gradient field in Maple.
- What are the equations of the flow lines for this gradient
field? In particular, what are the equations of the three
flow lines through the points (1,1,1), (1,1,2), and (1,1,3)?
- Plot these three flow lines in Maple, along with the isotimic
surfaces on the same graph.
- Section 3.3, page 124:
- 4, 5, 6, 11
- jh04.2:
- Let
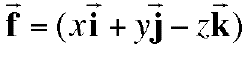 .
What is
.
What is 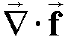 ?
?
- Plot a set of flow lines in the xz-plane. Do they appear
to be converging in some places and diverging in others? How can the
divergence of the vector field be constant? Plot the vector field in
the xz-plane, in order to assist with explanation.
SFU /
Math & Stats /
~hebron /
math252 /
assignments /
assgt04.html
Revised 31 January 1999 by
John Hebron.
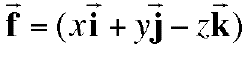 .
What is
.
What is 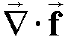 ?
?