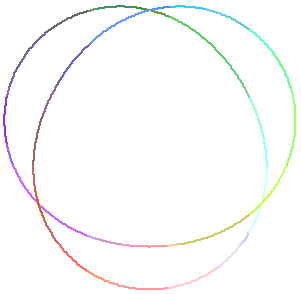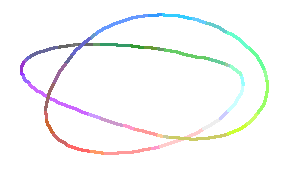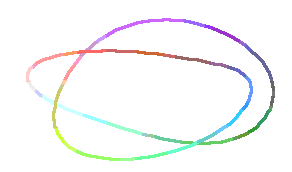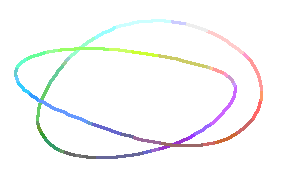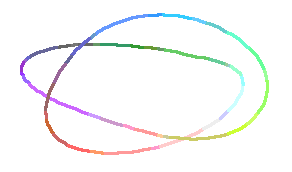Tim's Amazing Animation:

View From the Top:

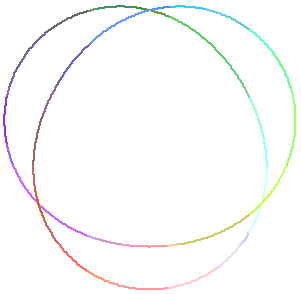
"View From the Top" was produced using the following Maple commands:

> x:=t->cos(t)*(cos(t*3/2)+6);
> y:=t->sin(t)*(cos(t*3/2)+6);
> z:=t->cos((t*3-Pi)/2);

                  x := t -> cos(t) (cos(3/2 t) + 6)


                  y := t -> sin(t) (cos(3/2 t) + 6)


                    z := t -> cos(3/2 t - 1/2 Pi)

> spacecurve([x(t),y(t),z(t)],t=0..4*Pi,axes='NONE',
>   orientation=[0,0],scaling='CONSTRAINED',
>   numpoints=1000,thickness=2);

View From the Front:

"View from the Front" was produced by viewing the above spacecurve at an orientation of [0,90]:

> spacecurve([x(t),y(t),z(t)],t=0..4*Pi,axes='NONE',
>   orientation=[0,90],scaling='CONSTRAINED',
>   numpoints=1000,thickness=2);

The Animation:

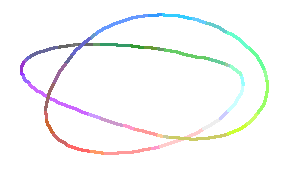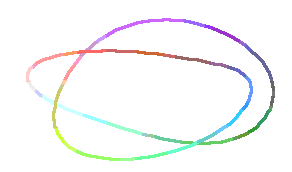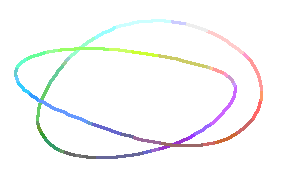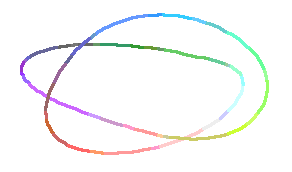
"The Animation" was produced by varying the angle at which the above spacecurve is viewed, using the following Maple commands:

> S:=seq(spacecurve([x(t),y(t),z(t)],t=0..4*Pi,axes='NONE',
>     orientation=[i*9,60],numpoints=200,
>     scaling='CONSTRAINED',thickness=2),i=0..40):
> display([S],insequence=true);