- 10, 18, 20, 30, 48, 54, 56
[Note: the problem shown in green is to be done using Maple. See the instructions below.]
- 10, 16 (convert the domain to Polar Coordinates), 18 (rationalize the numerator
and construct an epsilon-delta proof), 20, 26 (construct an epsilon-delta
proof), 30, 34, 44, 46
[Note: an epsilon-delta proof is required only for 18 and 26.]
- 20, 32, 38, 60, 72, 74, 76(e)
Staple these Maple Exercises to the end of all your handwritten work.
Some of the Maple Exercises involve handwritten work as well. In this case, do your handwritten work directly on the printed Maple Worksheet.
- Section 12.1
(See the posted 3-D Functions and Animations and the posted Exploring Cylindrical and Spherical Coordinates.)- 48: Plot the contour map in Maple,
(a 2-D contour plot is fine)
and then hand-draw arrows indicating the direction of increasing
contour levels.
- jh1: Animate a circular cylinder whose radius is modulated in
z-direction (as shown in Exploring
Cylindrical Coordinates) so that the sine ripples travel up along the z-axis
with time. Hand-in your code and a plot of the 1st frame of your animation.
- jh2: Animate a sphere whose radius is modulated by a sine term in phi (as shown in Exploring Spherical Coordinates) so that the ripples oscillate into and out of the sphere with time. Hand-in your code and a plot of the 1st frame of your animation (adjust your animation range so that the first frame shows something interesting, not just a featureless sphere).
- 48: Plot the contour map in Maple,
(a 2-D contour plot is fine)
and then hand-draw arrows indicating the direction of increasing
contour levels.
- Section 12.2
(See the posted Limits and Continuity.)- jh3: Explore the limit of the function
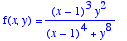 as
as 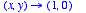 .
Plot in Maple and explain.
.
Plot in Maple and explain.
- jh3: Explore the limit of the function