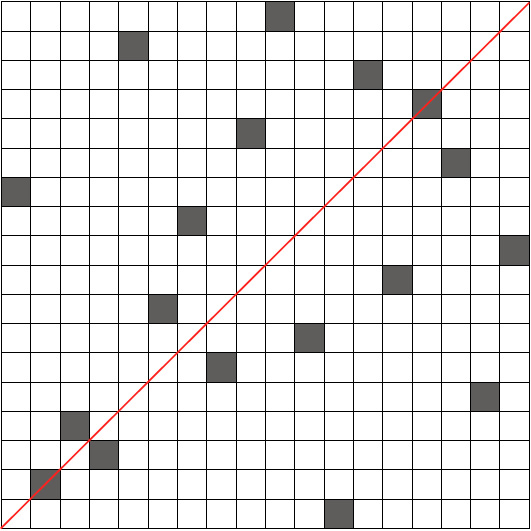
A symmetric Costas array of order 18 with anomalously small deficiency.
A Costas array is a permutation array for which no two line segments joining a pair of distinct ‘1’ entries have the same length and slope. This property can be used to control the frequencies of a sequence of sonar pulses, so that both the distance and velocity of a target can be correctly determined even in the presence of noise. Despite an extensive literature and massive computer searches, the only known constructions of Costas arrays are infinite families due to Welch (1982) and Golomb (1984), and minor variations. All 18,223 inequivalent Costas arrays of order at most 29 are known from exhaustive search, but only about 3% of those are explained by known constructions.
In 2014, Jane Wodlinger and I discovered numerically
that the
histogram of deficiency values for all Costas arrays of a given order
appears to isolate three classes of Costas arrays, only two of which
belong to known constructions; we suggested that the third class might
arise from an algebraic construction that has yet to be identified.
We also used combinatorial and probabilistic arguments to prove exact and
asymptotic results for when a Costas array can contain an
all-zero square corner region, proving a 2010 conjecture
due to Russo, Erickson and Beard.

A symmetric Costas array of order 18 with anomalously small deficiency.