Difference sets are highly structured objects whose study lies at
the intersection of design theory, coding theory, finite geometry
and algebraic number theory. Until 1997, the only groups for which
necessary and sufficient conditions were known for the existence of
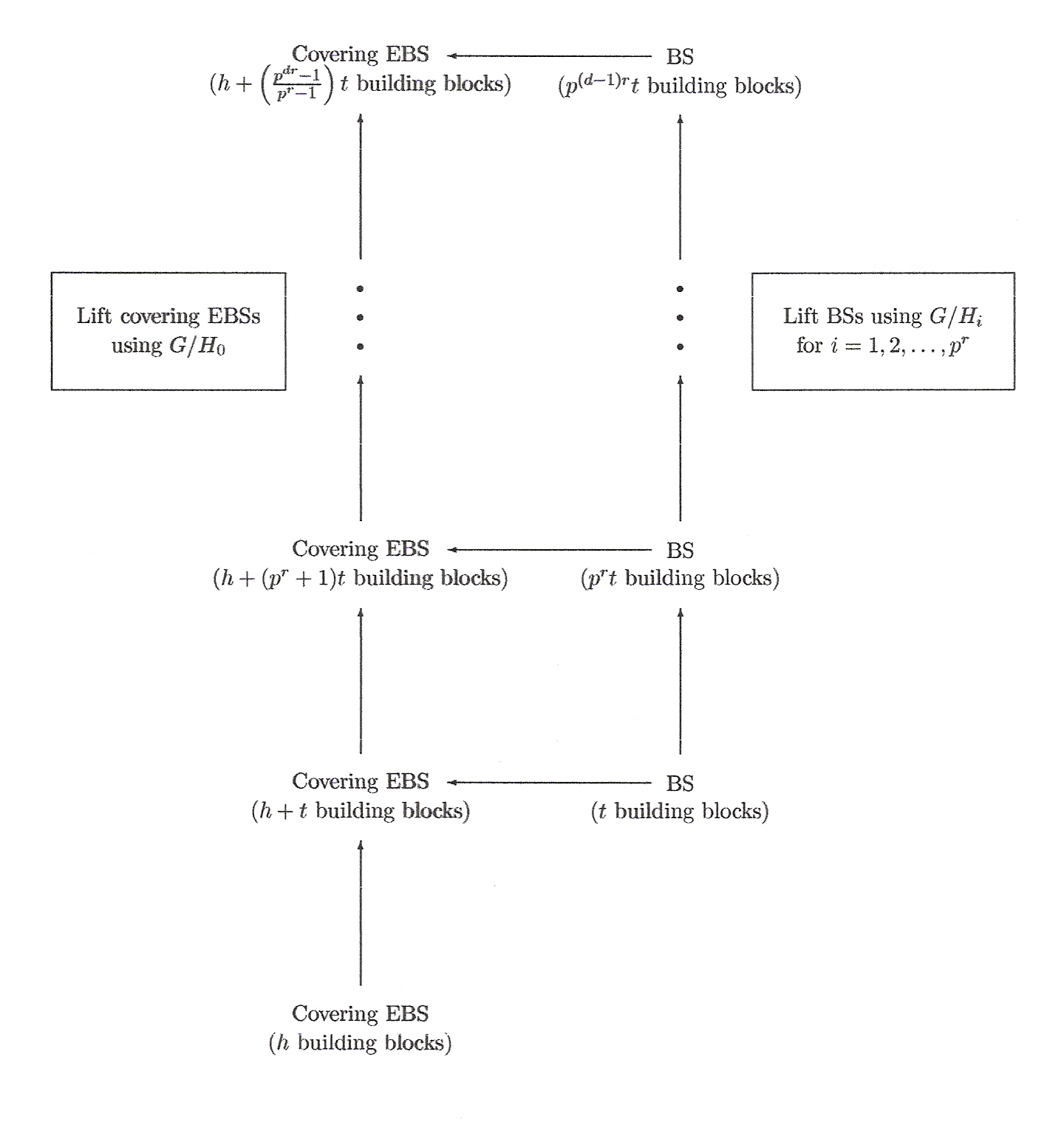
In 1997, Jim Davis and I presented a recursive construction for difference sets (and later gave a gentler overview) which unified the Hadamard, McFarland and Spence parameter families and dealt with all abelian groups known to contain such difference sets. We found a new infinite family of difference sets and included them in the unified framework. We also constructed new McFarland difference sets; when combined with a nonexistence result due to Ma and Schmidt, this gave necessary and sufficient conditions for an abelian group of order 22d+3(22d+1+1)/3 to contain a McFarland difference set.
Chen extended the construction to produce a further new parameter family of difference sets. Ionin developed it further to construct several new parameter families of symmetric designs.
