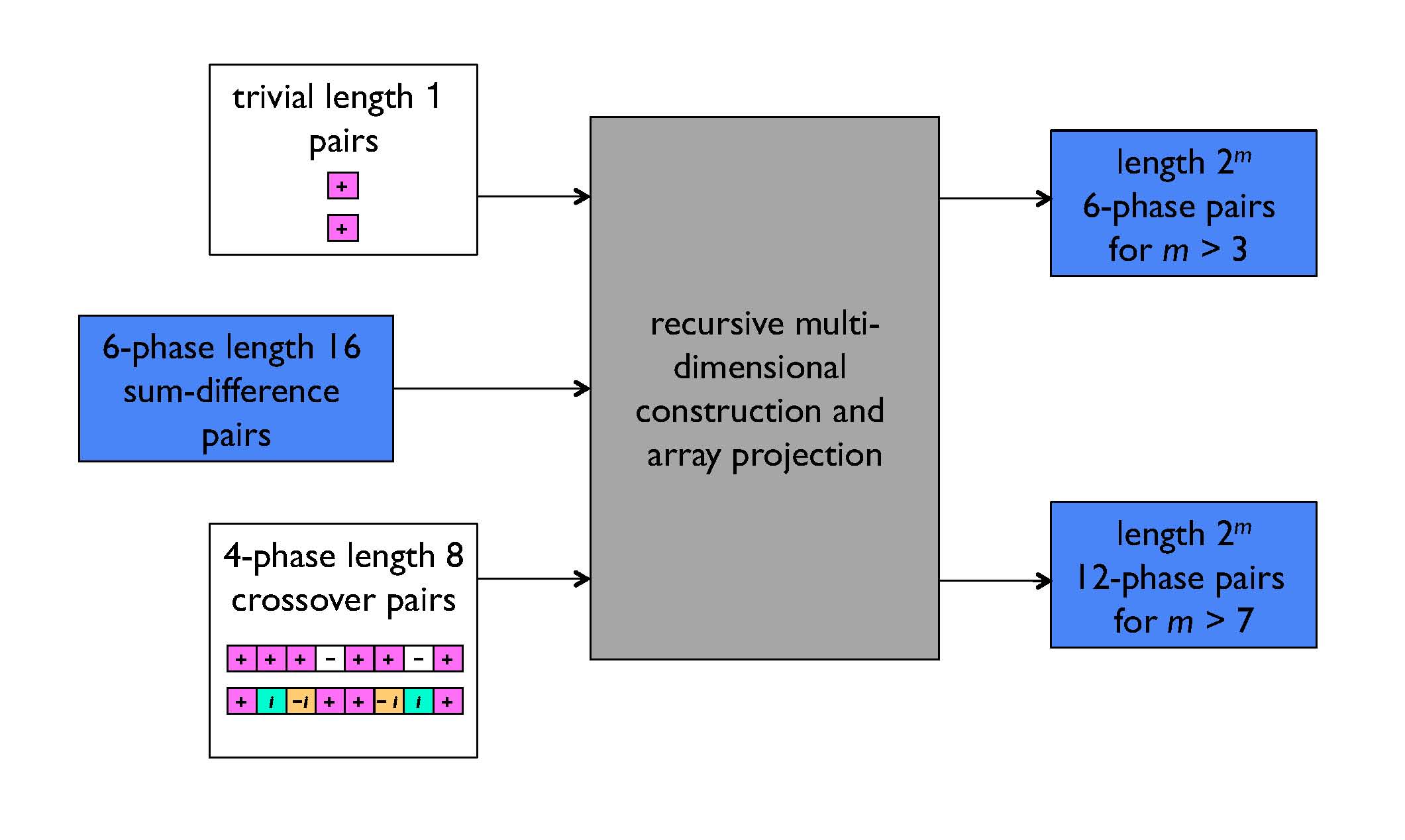
Construction of two new infinite families of Golay complementary sequences from 6-phase length 16 seed pairs.
Two sequences whose aperiodic autocorrelations sum to zero in all out-of-phase positions are called a pair of Golay complementary sequences, often defined over an alphabet of size 2 (binary), 4 (quaternary) or 8 (octary). Golay sequences have been used in many digital communication applications for which Barker sequences are not available, because they are known to exist for infinitely many lengths, even in the binary case.
In 1999, Jim Davis and I gave an explicit algebraic normal form for m!/2 · 2h(m+1) Golay sequences of length 2m over an alphabet of size 2h. It was believed for several years that there were no other Golay sequences for these lengths and alphabets, but in 2005 Ying Li and Wen Bin Chu unexpectedly found an additional 1024 length 16 quaternary Golay sequences by computer search. Frank Fiedler and I showed in 2006 that these new Golay sequences exist because of a shared autocorrelation property of certain quaternary length 8 Golay sequences, and that they spawn further new quaternary Golay sequences of length 32, 64, 128, …
Until 2007, the generalisation of a Golay sequence pair to the multi-dimensional case was studied in detail only by Melanie Dymond. In 2007, Matthew Parker and I showed that the projection of a multi-dimensional Golay array is a Golay sequence, and with Frank Fiedler we argued in 2008 that an array viewpoint is the natural way to construct and enumerate Golay sequences and pairs. This viewpoint accounts for all known Golay sequences and pairs of length 2m, including all quaternary Golay sequences spawned by Li and Chu's length 16 examples. Any new sources of sequences, such as the length 16 examples over an alphabet of size 6 that I discovered in 2010 with Frank Fiedler and Amy Wiebe, can be treated simply as additional “seed” pairs in the multi-dimensional construction.
