Jim Verner's Refuge for Runge-Kutta Pairs
Interaction in Research and Teaching:


Jim Verner
Ph.D., Edinburgh, October, 1969

My intentions
I have been interested in the derivation of new and better Runge-Kutta algorithms for some time. In particular, I showed that the design of Runge-Kutta pairs by E. Fehlberg could be improved to provide reliable algorithms for treating general initial value problems that might include substantial quadrature components, and constructed a design for generating such algorithms. My intention is to use this site to distribute some of the better algorithms I have derived. In recent years, I have been developing software for Ordinary Differential Equation Step-by-Step Solution Analysis (ODESSA). Some indication of progress on this project is indicated in items appearing later in this website.
Sets of all coefficients provided in attachments are copyrighted as such by the author. They many not be published for general distribution. They may be used for any research, industrial application or development of software provided that any product arising using any set of coefficients acknowledges this source and includes the URL for this site within the produced item.
Added October-November 2006
Modified November 2008
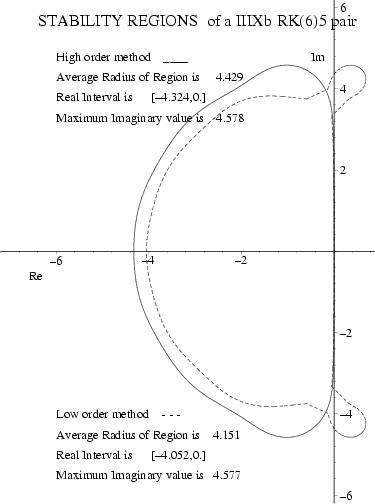
A "most efficient" Runge--Kutta (6)5 Pair with Interpolants
Click on ICON at right for stability regions.
- txt format: A most efficient RK 56 Pair
- txt format: Rational coefficients only
- txt format: Floating Point coefficients only
A "most robust" Runge--Kutta (6)5 Pair with Interpolants
Click on ICON at right for stability regions.
- txt format: A most robust RK 56 Pair
- txt format: Rational coefficients only
- txt format: Floating Point coefficients only

Added April, 2007:
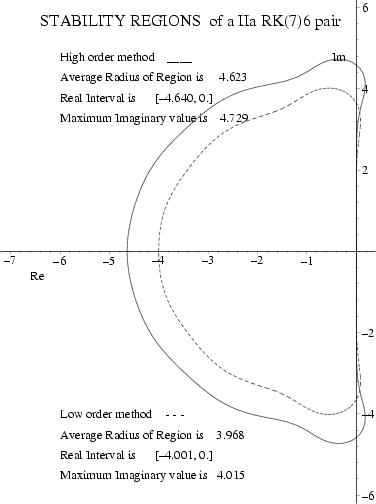
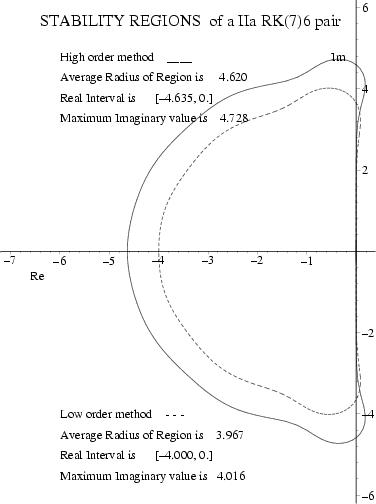
A "most efficient" Runge--Kutta (7)6 Pair with Interpolants
Click on ICON at right for stability regions.
- txt format: A most efficient RK 7(6) Pair
- txt format: Rational coefficients only
- txt format: Floating point coefficients only
A "most robust" Runge--Kutta (7)6 Pair with Interpolants
Click on ICON at right for stability regions.
- txt format: A most robust RK 7(6) Pair
- txt format: Rational coefficients only
- txt format: Floating point coefficients only

Added May, 2007:

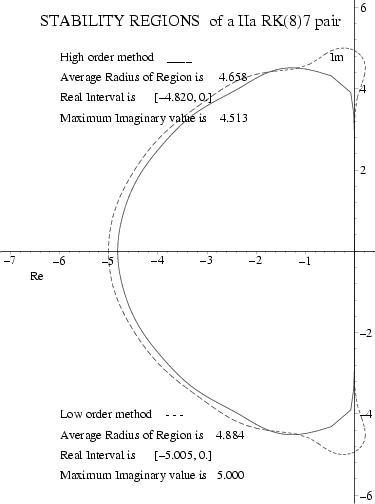
A "most efficient" Runge--Kutta (8)7 Pair with Interpolants
Click on ICON at right for stability regions.
- txt format: A most efficient RK 8(7) Pair
- txt format: Rational coefficients with floating point interpolants
- txt format: Floating point coefficients only
A "most robust" Runge--Kutta (8)7 Pair with Interpolants
Click on ICON at right for stability regions.
- txt format: A most robust RK 8(7) Pair
- txt format: Rational coefficients with floating point interpolants
- txt format: Floating point coefficients only

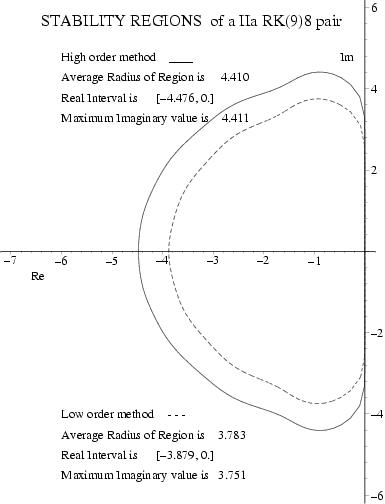
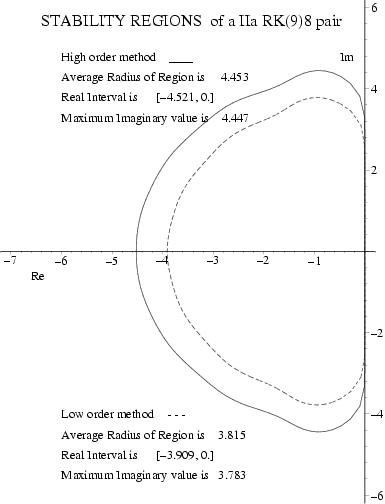
A "most efficient" Runge--Kutta (9)8 Pair with Interpolants
Click on ICON at right for stability regions.
- txt format: A most efficient RK 9(8) Pair
- txt format: Radical coefficients with floating point interpolants
- txt format: Floating point coefficients only
A "most robust" Runge--Kutta (9)8 Pair with Interpolants
Click on ICON at right for stability regions.
- txt format: A most robust RK 9(8) Pair
- txt format: Radical coefficients with floating point interpolants
- txt format: Floating point coefficients only
Added August, 2023:
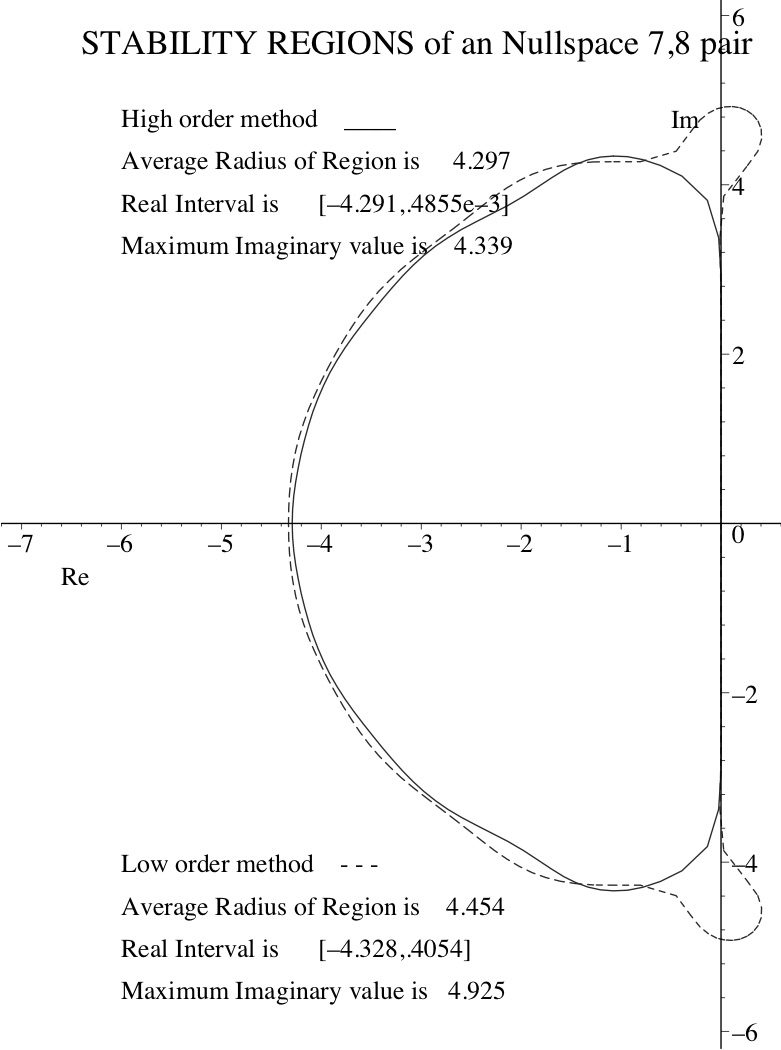
Coefficients for a (nearly) optimal nullspace explicit (8)7 Runge--Kutta pair
See Recent manuscript 1. below.
Click on ICON at right for stability regions.
- txt format: A nullspace efficient RK 8(7) Pair

Coefficients for a TSRK6 method with starting methods
See Refereed Journal Article 10. below.
- txt format: TSRK6 method with starting methods

Current University Affiliations:
Adjunct Professor
- Department of Mathematics
Simon Fraser University
8888 University Avenue,
Burnaby, B.C., Canada, V5A 1S6Professor Emeritus
- Department of Mathematics and Statistics
Queen's University at Kingston
Kingston, Ontario, Canada, K7L 3N6
- E-mail:
- jimverner@shaw.ca
- Office:
- Science Building, Room K9505.3, Simon Fraser University
- Phone:
- (778)782-3009
- Personal Interests:
- Bridge, Photography, Hiking, Canoeing, Skiing
Teaching
Sept. 1963 - April 1964: Royal Military College Kingston, Ontario Sept. 1964 - July, 1966: Government College, Umuahia, Nigeria Sept. 1969 - Dec. 2000: Queen's University Department of Mathematics and Statistics Sept. 2001 - April 2008: Simon Fraser University Department of Mathematics
Research interests
Numerical analysis, integration methods for systems of ordinary differential equations
Research groups:
Pacific Institute of Mathematical Sciences Centre for Scientific Computation Algorithms
Trees.TSRK.maple: A MAPLE code for order conditions and assessment of Two-Step Runge--Kutta (TSRK) methods.
(This code generates the order conditions of arbitrary order for a TSRK method, and provides coefficients of error
espressions which may be used to contrast a TSRK method with any other method for potential efficiency. See below.)
Conference Presentations
Feb. 2023, ANODE2023, University of Auckland, NZ
Nullspaces yield new explicit Runge--Kutta methods- pdf format: Abstract
Feb. 2018, ANODE2018, University of Auckland, NZ
ODESSA - Software for the Analysis of General Linear Methods- pdf format: Abstract
Jan. 2013, ANODE2013, University of Auckland, NZ
New Runge--Kutta pairs of lower stage-order- pdf format: Abstract
July 2011, University of Toronto, Ontario;
A retrospective on the derivation of Runge--Kutta pairs- pdf format: Abstract
May 2009, NTNU, Trondheim, Norway;
June 2009, Department of Mathematics, Laurentian University, Sudbury, Ontario
B-series and TSRK pairs based on Gaussian quadratures- pdf format: Abstract
July 2008, GLADE: Conference on General Linear Algorithms for Differential Equations, Auckland, New Zealand
B-series and TSRK methods based on Gaussian Quadrature- pdf format: Abstract
July, 2007, SciCADE07, St. Malo, France
Numerically Optimal Runge--Kutta Pairs and Interpolants- pdf format: Abstract
July, 2005, SciCADE05, Nagoya, Japan
Order Tests and Derivation of Two-Step Runge--Kutta Pairs of Order 8- pdf format: Abstract
May, 2004, Conference on Numerical Volterra and Delay Equations, Tempe, Arizona
Improved Starting Methods for Two-step Runge--Kutta Methods- pdf format: Abstract
July,2003, ANODE03, Auckland, New Zealand
Starting Methods for High-order Two-step Runge--Kutta Methods- pdf format: Abstract
December, 2002, WODE, Bari, Italy
Why are some Two-step Runge--Kutta Methods Inaccurate?- pdf format: Abstract
Research Publications
Recent Manuscripts
J.H. Verner, Nullspaces yield new explicit Runge--Kutta pairs, (2023) 26 pages.
- Springer Preview: Nullspaces yield new explicit Runge--Kutta pairs
Refereed Journal Articles
A. Cardone, Z. Jackiewicz, J.H. Verner, B. Welfert, Order conditions for general linear methods, J. Applied Mathematics and Computation 290, (2015), pp. 44--64.
https://doi.org/10.1016/j.cam.2015.04.042
- Abstract: Order conditions for general linear methods
- J.H. Verner, Explicit Runge--Kutta pairs with lower stage-order. Numerical Algorithms, 65, (2014) pp. 555--577.
https://doi.org/10.1007/s11075-013-9783-y
- Abstract: Explicit Runge--Kutta pairs with lower stage-order
- Springer Preview: Explicit Runge--Kutta pairs with lower stage-order
- Yiannis Hadjimichael, Colin B. Macdonald, David I. Ketcheson, James H. Verner, Strong stability preserving explicit Runge--Kutta methods of maximal effective order, SIAM J. NA, 51, No. 4 (2013) pp. 2149--2165. https://doi.org/10.1137/120884201
- Abstract: SSP explicit Runge--Kutta methods of maximal effective order
- SIAM NA Preview: SSP explicit Runge--Kutta methods of maximal effective order
- Anne Kværnø and Jim Verner, Subquadrature Expansions for TSRK methods. Numerical Algorithms, 59, (2012) pp. 487--504.
https://doi.org/10.1007/s11075-011-9500-7
- Springer Preview: Subquadrature Expansions for TSRK methods
- Anne Kværnø and Jim Verner, Trees.TSRK.maple: a MAPLE code for order conditions and assessment of Two-Step Runge--Kutta (TSRK) methods.
- numeralgo/na32.tgz Netlib Repository (2012).
- Download the zip folder from the library. This folder contains instructions in a README.txt file.
- Numeralgo Library: na32.tgz
- J.H. Verner, Numerically optimal Runge--Kutta pairs with interpolants. Numerical Algorithms, 53, (2010) pp. 383--396.
https://doi.org/10.1007/s11075-009-9290-3
- Abstract: Numerically optimal Runge--Kutta pairs with interpolants
- Springer Preview: Numerically optimal Runge--Kutta pairs with interpolants
- J.H. Verner, Improved Starting methods for two-step Runge--Kutta methods of stage-order p-3, Applied Numerical Mathematics, 56, (2006) pp. 388--396.
https://doi.org/10.1016/j.apnum.2005.04.028
- APNUM Preview: Improved starting methods of stage-order p-3
- J.H. Verner, Starting methods for two-step Runge--Kutta methods of stage-order 3 and order 6, J. Computational and Applied Mathematics, 185, (2006)
pp. 292--307. https://doi.org/10.1016/j.cam.2005.03.012
- Elsevier Preview Starting methods for two-step Runge--Kutta methods of stage-order 3 and order 6
- T. Macdougall and J.H. Verner, Global error estimators for order 7,8 Runge--Kutta pairs, Numerical Algorithms 31, (2002) pp. 215--231.
https://doi.org/10.1023/A:1021190918665
- Num. Alg. Preview Global error estimators for order 7,8 Runge--Kutta pairs.
- Z. Jackiewicz and J.H. Verner, Derivation and implementation of two-step Runge--Kutta pairs. Japan Journal of Industrial and Applied Mathematics 19 (2002), pp. 227--248. https://doi.org/10.1007/BF03167454
- JJIAM Preview Derivation and implementation of two-step Runge--Kutta pairs
A corrected form of this paper is- pdf: Derivation of TSRK Methods
- P.W. Sharp and J.H. Verner, Some extended Bel'tyukov pairs for Volterra integral equations of the the second kind, SIAM Journal on Numerical Analysis 38 (2000), pp. 347--359. https://doi.org/10.1137/S003614299631280X
- SIAM J. NA Preview: Some extended Bel'tyukov pairs for Volterra integral equations of the the second kind
- P.W. Sharp and J.H. Verner, Extended explicit Bel'tyukov pairs of orders 4 and 5 for Volterra integral equations of the the second kind, Applied Numerical Mathematics 34 (2000), pp. 261--274. https://doi.org/10.1016/S0168-9274(99)00132-4
- ANM Preview Extended explicit Bel'tyukov pairs of orders 4 and 5 for Volterra integral equations of the the second kind
- D.D. Olesky, P. van den Driessche and J.H. Verner, Graphs with the same determinant as a complete graph, Linear Algebra and its Applications 312 (2000),
pp. 191--195. https://doi.org/10.1016/S0024-3795(00)00114-2
- Elsevier Preview Graphs with the same determinant as a complete graph,
- P.W. Sharp and J.H. Verner, Generation of High Order Interpolants for Explicit Runge--Kutta Pairs, AMS Transactions on Mathematical Software 24 (1998), pp.13--29. https://doi.org/10.1145/285861.285863
- AMS ToMS Preview Generation of High Order Interpolants for Explicit Runge--Kutta Pairs
- J.H. Verner, High order explicit Runge--Kutta pairs with low stage order, Applied Numerical Mathematics 22 (1996), pp. 345--357.
https://doi.org/10.1016/S0168-9274(96)00041-4
- ANM Preview High order explicit Runge--Kutta pairs with low stage order
- J.H. Verner and M. Zennaro, The orders of embedded continuous explicit Runge--Kutta methods, BIT 35 (1995), pp. 406--416.
https://doi.org/10.1007/BF01732613
- Springer Preview: The orders of embedded continuous explicit Runge--Kutta methods
- J.H. Verner and M. Zennaro, Continuous explicit Runge--Kutta methods of order 5, Mathematics of Computation 64 (1995), pp.1123--1146.
https://doi.org/10.2307/2153486
- Math. Comp. Preview Continuous explicit Runge--Kutta methods of order 5
- J.H. Verner, Strategies for deriving new explicit Runge--Kutta pairs, Annals of Numerical Mathematics 1 (1994), pp. 225--244.
- pdf format: Strategies for deriving new explicit Runge--Kutta pairs
- P.W. Sharp and J. H. Verner, Completely imbedded Runge--Kutta pairs. SIAM J. NA 31 (1994), pp. 1169--1190. https://doi.org/10.1137/0731061
- SIAM J. NA Preview Completely imbedded Runge--Kutta pairs
- J.H. Verner, Differentiable interpolants for high-order Runge--Kutta methods. SIAM J. NA 30 (1993), pp.1446--1466. https://doi.org/10.1137/0730075
- SIAM J. NA Preview Differentiable interpolants for high-order Runge--Kutta methods
- J.H. Verner, Some Runge--Kutta formula pairs, SIAM J. NA. 28 (1991), pp. 496--511. https://doi.org/10.1137/0728027
- SIAM J. NA Preview Some Runge--Kutta formula pairs
- J.H. Verner, A contrast of some Runge--Kutta formula pairs, SIAM J. NA. 27 (1990), pp. 1332--1344. https://doi.org/10.1137/0727076
- SIAM J. NA Preview A contrast of some Runge--Kutta formula pairs
- J.H. Verner, Families of imbedded Runge--Kutta methods, SIAM J. NA. 16 (1978), pp. 875--885. https://doi.org/10.1137/0716064
- SIAM J. NA. Preview Families of imbedded Runge--Kutta methods
- J.H. Verner, Explicit Runge--Kutta methods with estimates of the local truncation error, SIAM J. NA. 15 (1978), pp. 772--790. https://doi.org/10.1137/0715051
- SIAM J. NA. Preview Explicit Runge--Kutta methods with estimates of the local truncation error
- A.V. Geramita and J.H. Verner, Orthogonal designs with zero diagonal, Canadian J. Math. 28 (1976), pp. 215--224. https://doi.org/10.4153/CJM-1976-028-3
- Can. J. Math. Preview Orthogonal designs with zero diagonal
- G.J. Cooper and J.H. Verner, Some explicit Runge--Kutta methods of high order, SIAM J. NA. 9 (1972), pp. 389--405. https://doi.org/10.1137/0709037
- SIAM J. NA Preview Some explicit Runge--Kutta methods of high order
- J.H. Verner, Quadratures for implicit differential equations, SIAM J. NA. 7 (1970), pp. 373--385. https://doi.org/10.1137/0707030
- SIAM J. NA Preview Quadratures for implicit differential equations
- J.H. Verner, The order of some implicit Runge--Kutta methods, Numerische Mathematik 13 (1969), pp. 14--23. https://doi.org/10.1007/BF02165270
- Num. Math. Preview The order of some implicit Runge--Kutta methods
- J.H. Verner and M.J.M. Bernal, On generalizations of the theory of consistent orderings for successive over--relaxation methods, Numerische Mathematik 12 (1968), pp. 215--222. https://doi.org/10.1007/BF02162914
- Num. Math. Preview On generalizations of the theory of consistent orderings for successive over--relaxation methods
Conference Proceedings
- J.H. Verner, A classification scheme for studying explicit Runge Kutta pairs, Scientific Computing, S. O. Fatunla (editor), Ada and Jane Press, Benin City, Nigeria, 1994, 201-225.
- pdf format: Classification of RK pairs
- J.H. Verner, A comparison of some Runge--Kutta formula pairs using DETEST, Computational Ordinary Differential Equations, S.O. Fatunla (editor), Univ. Press PLC, Ibadan, Nigeria, 1991, pp. 271--284.
- pdf format: A comparison of some Runge--Kutta formula pairs using DETEST
- J.H. Verner, John Butcher's algebraic theory: Motivation for selecting simplifying conditions, Proceedings of the Ninth Manitoba Conference on Numerical Mathematics, Winnipeg, Manitoba, 1979, pp. 125-155.
- J.H. Verner, Selecting a Runge--Kutta method, Proceedings of the Sixth Manitoba Conference on Numerical Mathematics, Winnipeg, Manitoba, 1976, pp. 495--504.
- J.H. Verner, On deriving certain hybrid methods, Proc. Manitoba Conf. on Numerical Mathematics, Winnipeg, Manitoba, 1971, pp. 607--626.
- J.H. Verner, On deriving explicit Runge--Kutta methods, Proc. on Applications of Numerical Analysis, Dundee, Scotland, 1971, pp. 341--347.
- J.H. Verner, Implicit methods for implicit differential equations, Proc. of the Conference on the Numerical Solution of Differential Equations, Dundee, Scotland, 1969, pp. .
Other Research Reports
- P. Chartier, E. Lapôtre, J.H. Verner, Reversible B-series and the derivation of pseudo-symmetric Runge--Kutta methods, INRIA report , Campus de Beaulieu, Rennes, France, 2000, 23 pages.
- J.H. Verner, The derivation of high order explicit Runge--Kutta methods, Department of Mathematics Report No. 93, University of Auckland, New Zealand, 1976, 27 pages.
- J.H. Verner, Convergence of a finite difference scheme fora second order ordinary differential equation with a singularity, London Institute of Computer Science Report ICS/001/1967 (1967), 19 pages.
Stories with John
After I had studied a number of John Butcher's papers during my Ph.D. program, he and I met at my home in Kingston, Canada in December, 1969. At that time he dictated an algorithm in Algol, and I coded it in APL to provide a general procedure for verifying the algebraic order of a Runge--Kutta method. Over many years often at ANODE conferences, we have worked together informally on a variety of Runge--Kutta and other methods. Since the launch of his recent monograph in April, 2021, we have agreed to review some of our interactions, and these are being presented as short stories on his website, jcbutcher.com .
- Jim Verner, The first eighth order method, jcbutcher.com/p8
- John Butcher and Jim Verner, Our first B-series program, jcbutcher.com/1970
- Jim Verner, APL to MAPLE code of RKTest70.APL, jcbutcher.com/node/100
- Jim Verner, Deriving new explicit Runge--Kutta pairs using Test21, jcbutcher.com/node/102
Last modified Aug. 8, 2023.
Algorithms to and from jimverner@shaw.ca