Department of Mathematics
Spring 2004
APMA 935 - Mathematical Modelling
Week 00
Announcements:
05 January
syllabus (pdf)
info form (pdf), please bring completed form to first lecture
11 December
first lecture: 06 january, 9:30-11:30, SSC8666
Abstract:
22 October
abstract (link), (pdf)
A Mathematical View of Modern Science
Development of the theory of partial differential equations (PDEs) was one of
the key influences behind the scientific revolution of the late 19th-century
as it brought a powerful quantitative tool for the study of many problems in
modern science. A complete applied mathematical
study addresses two issues: translation of the scientific context with model
equations (derivation & interpretation), and investigation of the mathematical
properties of these equations (analysis, solution & computation). In this
course, methods for the derivation, solution and computation of PDE models
are discussed within the context of familiar examples from the physical sciences.
The lectures will discuss how the basic linear PDE trilogy, the diffusion,
potential & wave equations, naturally arise in scientific theories such as probability,
gravity and sound propagation. The analysis of these equations will also be revisited
through the development of various solution techniques: eigenfunction expansions,
Greens functions and integral transforms. Later lectures will present
advanced examples involving systems of PDEs and nonlinearity.
Computer visualization will be an important accompaniment to the lectures and
assigned work. Methods for numerical computing and graphics will be
introduced through the use and modification of downloadable Matlab scripts.
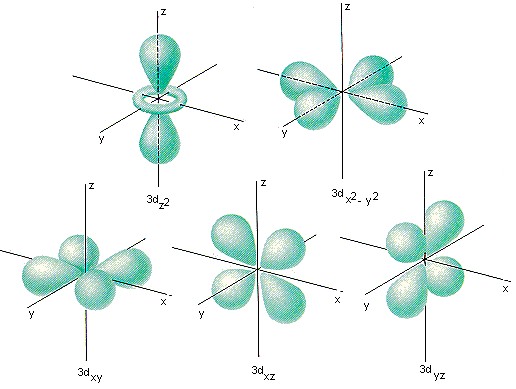
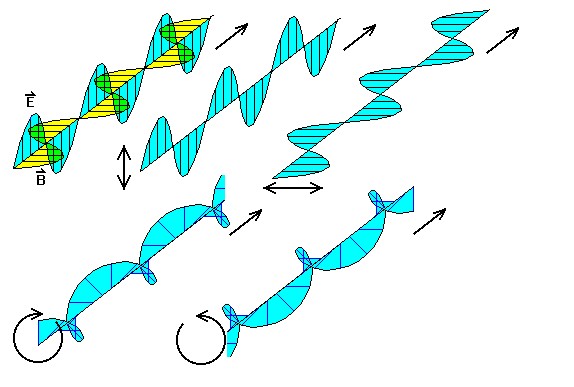
The images below are illustrations of magnetic field lines, electron
orbitals and polarized light waves. The mathematical theories associated with these
phenomena involve the Poisson, Schrodinger and Maxwell equations.
Images & Interest:
magnetic field lines
electron orbitals
polarized light wave