revisiting Queney's flow over a mesoscale ridge (pdf preprint)
revisiting Queney's flow over a mesoscale ridge (pdf preprint) 
The most familiar illustrations of downstream topographic waves are the streamline plots from the original linear wave studies of Queney. For steady flow past a two-dimensional ridge, Queney's downstream radiation patterns were obtained through approximations of the Fourier integral which describes the dispersion of linear gravity waves. In the case of constant stratification with rotation, a high-accuracy numerical quadrature of the Fourier integral reveals significant departures in the near-ridge streamfunction pattern from the original depictions. This numerical accuracy is achieved by a specialized quadrature scheme for computing the singular Fourier integrals encountered in this regime of order-one Rossby number. In addition, a steepest descent approximation is presented which resolves the breakdown of Queney's analysis above of the summit and quantifies the unusually weak decay of wave amplitude with height.
 revisiting Queney's flow over a mesoscale ridge (pdf preprint)
revisiting Queney's flow over a mesoscale ridge (pdf preprint)
 Queney's displacement streamlines (pdf figure)
Queney's displacement streamlines (pdf figure)  displacement streamlines recomputed (pdf figure, gzip eps)
displacement streamlines recomputed (pdf figure, gzip eps) 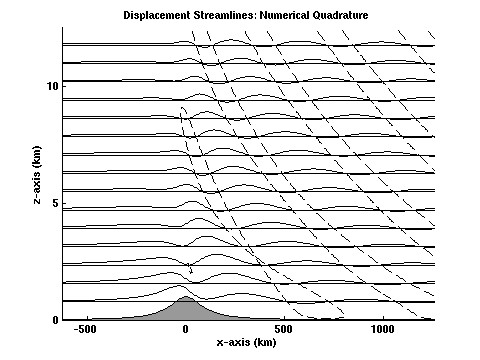
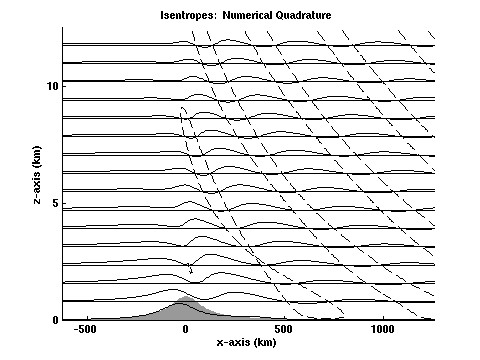
 isentropes recomputed (pdf figure, gzip eps)
isentropes recomputed (pdf figure, gzip eps) at moderate Rossby number (R=1) there is significant difference between the linearized BC and
the true topography
at moderate Rossby number (R=1) there is significant difference between the linearized BC and
the true topography