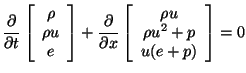
The plots below illustrate the difference between computations on a moving mesh (left) and a fixed grid (right), both with the same number of grid points. The partial differential differential equations being solved are the Euler equations of gasdynamics:
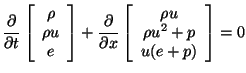
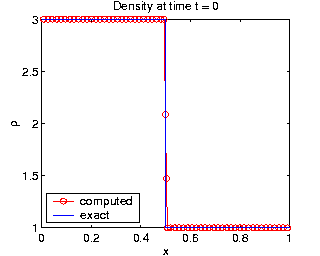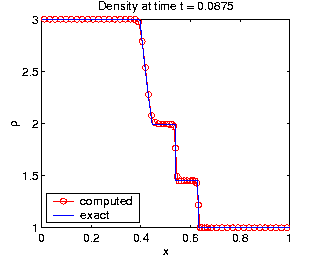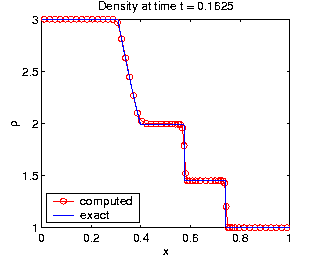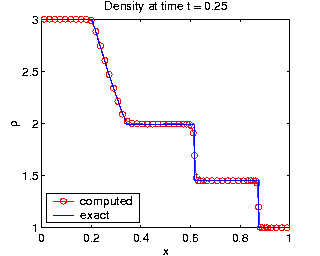
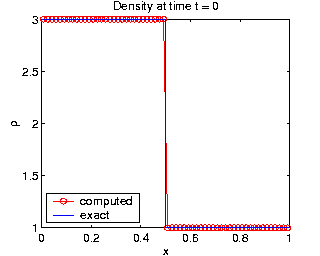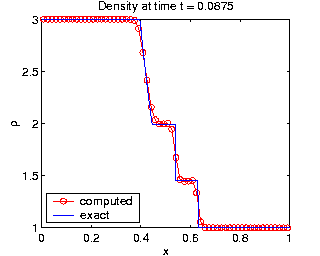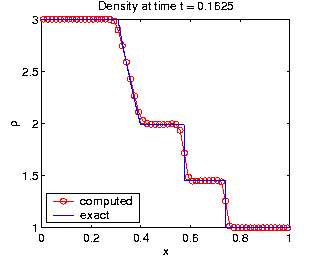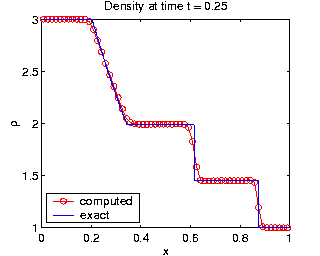
The plots of density, 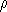 , clearly
demonstrate that the moving mesh method resolves all three solution
features more accurately using the same number of grid points.
The moving mesh method clearly displays much better shock resolution,
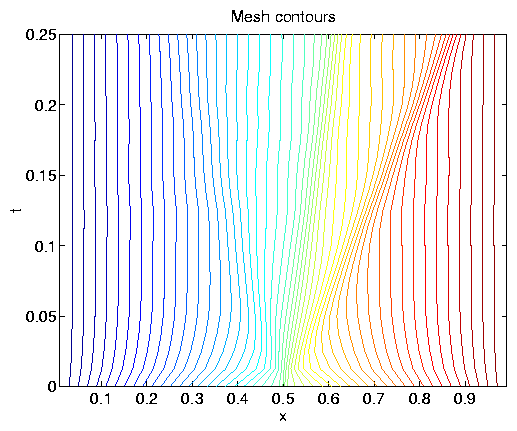
and the plot of the mesh trajectories (at bottom) indicates how mesh
points smoothly cluster together as the discontinuity develops, and then
follow along with the shock. The mesh contours at the bottom indicate
how the mesh points track the shock and contact line.
, clearly
demonstrate that the moving mesh method resolves all three solution
features more accurately using the same number of grid points.
The moving mesh method clearly displays much better shock resolution,
and the plot of the mesh trajectories (at bottom) indicates how mesh
points smoothly cluster together as the discontinuity develops, and then
follow along with the shock. The mesh contours at the bottom indicate
how the mesh points track the shock and contact line.
| Moving mesh solution (N=60) | Fixed mesh solution (N=60) |
|---|---|
 |
 |
 |
| [ Home ] | Last modified: Tue Dec 15 2009 |