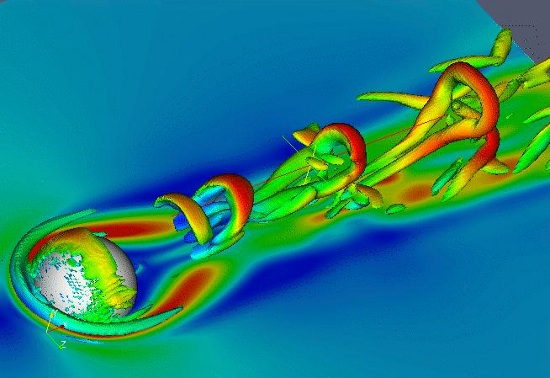
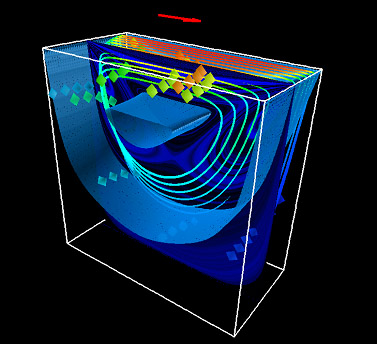
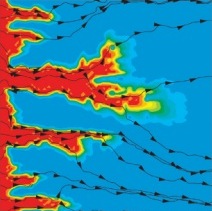
| Flow over a cylinder. | Lid-driven cavity flow. | Fingering in a porous medium. |
 |
 |
 |
| John Stockie |
| Department of Mathematics, SFU |
| Office: K 10518 |
| Tel: +1 778 782 3553 |
| stockie@math.sfu.ca |
| Time: | Tuesdays and Thursdays, 2:30-4:20 |
| Location: | AQ 5008 |
This course will introduce students to a variety of computational approaches for solving the partial differential equations governing fluid dynamics, focusing on finite difference and finite volume techniques. Theoretical background material will be introduced as necessary, but the emphasis of the course will be on the numerical methods, their accuracy and stability, and applying them in practical calculations of real fluid flows. Students will gain experience writing their own codes, as well as employing existing open-source software packages. Applications will be drawn from a wide variety of problems arising in wave propagation, incompressible fluids, compressible gas dynamics, and porous media flow. In contrast with the common engineering approaches to teaching CFD, I will not emphasize the study of complex flows in sophisticated geometries using commercial codes, but will focus instead on the design of the underlying algorithms, and carefully assessing their correctness, accuracy, efficiency and robustness.
Previous courses in ordinary and partial differential equations (such as MATH 310 or MATH 314) are required, as is some experience in computer programming (any language is fine although knowledge of MATLAB would be particularly helpful). A previous course in fluid dynamics (such as MATH 462) would be an advantage, but is not required.
| Flow over a cylinder. | Lid-driven cavity flow. | Fingering in a porous medium. |
 |
 |
 |
The grade for this course will be made up of homework assignments (60%) and a project (40%). There is no final examination.
There is no textbook for this course. Material will be drawn from a number of texts, some of which are held on reserve in the library:
| Last modified: Wed Jan 16 2019 |