I'm In ... No, I'm Out: Part IV

Brian Alspach

Poker Digest Vol. 2, No. 17, August 13 - 26, 1999

In the first three parts of this series, we have explored the use of the principle of inclusion-exclusion. Now we get to the reason for introducing the topic in the first place; namely, we want to determine the probability no one is a dealt a pair in hold'em. This certainly is the most sophisticated of the twenty-seven articles to appear thus far in Poker Digest, but each step can be followed if you keep in mind the basic context for inclusion-exclusion and the reason each step makes sense. First, let's establish the scenario in which inclusion-exclusion becomes the tool of choice.

First, we are going to derive a general formula so let's assume there are n players. Normally, n will be 9, 10 or 11, but if the game is shorthanded, n may be smaller.

Let P_i denote the property player i is dealt a pocket pair. We are interested in counting the number of ways no one has a pair, that is, none of the properties $P_1,P_2,\ldots,P_n$ holds. This is exactly the classical setting for applying inclusion-exclusion. We also require counting the number of ways in which a prescribed subset of properties can hold to be easy. We shall see this is the case.

For this problem the players are labelled 1,2,...,n because we are defining our properties in terms of particular players. Recall that semi-deals refer to dealing cards to players without regard to which players get which hands. In the present case, we are interested in which players get which cards and, thus, we are interested in the number of deals rather than the number of semi-deals. In most cases counting problems involving labelled objects is easier than counting problems with unlabelled objects and that is the case here too. In other words, we want to know how many ways n labelled players may be dealt two cards each. The first player can receive two cards in C(52,2) ways, the second player in C(50,2) ways and so on until the n-th player can receive two cards in C(50-2n+2,2) ways. Multiplying these numbers yields

$\begin{displaymath}\frac{52!}{(52-2n)!2^n}\end{displaymath}$

ways n labelled players may be dealt two cards each. The same principle applies if fewer cards are being dealt to a subset of players.

Now we let M(S) denote the number of deals in which a given subset S of players receive a pair, that is, for each $i\in S$ the property P_i holds. Under this notation, $M(\emptyset)$ denotes the total number of ways of dealing two cards to each of n people.

The principle of inclusion-exclusion then tells us that the number of deals in which none of the properties are satisfied, or the answer to the question, is

$\begin{displaymath}\sum_S (-1)^rM(S),\end{displaymath}$

where the sum is over all subsets S of an n-set, and r denotes the number of elements in S. It is easy to see that M(S) is the same for any two subsets S having the same number of elements. Thus, let M(r) denote M(S) for any subset S with r elements. The previous sum then becomes

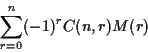
$\begin{displaymath}\sum_{r=0}^n (-1)^rC(n,r)M(r)\end{displaymath}$

because there are C(n,r)subsets with r elements.

The preceding equation expresses the number of deals to n players in which no one receives a pair. This reduces the problem to that of calculating M(r). In other words, the problem is reduced to determining how many deals give a fixed set of r players pairs (where what the remaining n-r players get is not restricted). There is a complication arising here because some of the rplayers may get pairs of the same rank. How do we handle this?

Remember we are working with an arbitrary value of n. In fact, what are the restrictions on n? First, n must be at least 1 as it does not make much sense to deal cards to fewer than 1. Second, n is at most 26 because there are only 52 cards in the deck. Thus, $1\leq n \leq 26$ .

Suppose there are t pairs of players who receive pairs of the same rank. What kinds of restrictions are there on t? It is easy to see that $2t\leq r$ because the t pairs of players comprise 2t players and there are only r players available. This implies $t\leq\lfloor r/2 \rfloor$ . (The notation $\lfloor r/2\rfloor$ means the integer part of r/2. For example, $\lfloor 7/2\rfloor = 3$ .) There are only 13 ranks from which to choose pairs so that if $r\geq 13$ , there must be at least r-13 ranks which occur as pairs in two different hands. Since t is not negative, we must have $t\geq\mathrm{max}\{0,r-13\}$ . This gives us the restriction that t satisfies $\mathrm{max}\{0,r-13\}\leq t\leq \lfloor r/2\rfloor$ ,

Hence, for each t satisfying $\mathrm{max}\{0,r-13\}\leq t\leq \lfloor r/2\rfloor$ , there may be t pairs of people who receive pairs of the same rank using all four cards of the same rank. From r people there are C(r,2t) ways to choose the 2t people who will get pairs of the same rank as somebody else. From amongst these 2t people we must choose the pairs of people who will receive pairs of of the same rank. We can choose the first pair of people in C(2t,2) ways, the next pair of people in C(2t-2,2) ways and so on until only two people are left who form the final pair. Multiplying all these numbers and dividing by t! because it doesn't matter in which order they are chosen yields

$\begin{displaymath}\frac{(2t)!}{t!\;2^t}\end{displaymath}$

ways of choosing the pairs of people to get pairs of the same rank.

(Stay tuned for Part V)

website by the Centre for Systems Science
last updated 27 August 2001