I'm In ... No, I'm Out: Part 5

Brian Alspach

Poker Digest Vol. 2, No. 18, August 27 - September 29, 1999

In the last issue, recall that we are determining the probability no one is a dealt a pair in hold'em when there are n hands dealt. We are using the Principle of Inclusion-Exclusion to count the number of ways no one is dealt a pair from which we shall derive the probability. We let Pi denote the property player i is dealt a pocket pair. We saw that

\begin{displaymath}C(n,0)M(0)-C(n,1)M(1)+C(n,2)M(2)-\cdots+ (-1)^nC(n,n)M(n)\end{displaymath}

is the number of deals for which no one receives a pair, where M(r) is the number of ways in which a specified set of r players is dealt a pair with no restriction on the cards the remaining n-r players receive. This reduces the problem to the determination of M(r).

As a first step towards determining M(r), we saw that for each t from $\mathrm{max}\{0,r-13\}$ through the integer part of r/2, there are $(2t)!/(t!\;2^t)$ ways of choosing t pairs of people (subsequently referred to as couples) to receive pairs of the same rank. That is where we stopped in the last issue.

Once the couples have been formed, there are C(13,t) ways of picking which ranks of cards will be assigned to the t couples. These tranks can be assigned in t! ways to the t couples. Once the ranks have been assigned to the couples, there are six ways to split the four cards of the same rank amongst a given couple. Hence, there are 6t ways for the pairs to be distributed amongst the t couples. Therefore, there are

\begin{displaymath}C(r,2t)C(13,t)\frac{(2t)!\,t!\,6^t}{t!\,2^t}\end{displaymath}

deals in which precisely 2t people from r receive a pair of the same rank as someone else.

The remaining r-2t people must get pairs of distinct ranks. There are C(13-t,r-2t) choices for the ranks. Each choice of ranks can be assigned in (r-2t)! ways to the players and each assignment can have any of six pairs of a given rank yielding 6r-2t deals for each assignment of ranks. Finally, the remaining n-r people can be dealt any two cards from the remaining 52-2r cards. This can be done in $(52-2r)!/(52-2n)!\,2^{n-r}$ ways. Altogether, this yields

\begin{displaymath}C(r,2t)C(13,t)C(13-t,r-2t)\frac{(2t)!\, t!\,(r-2t)!\,(52-2r)!\,6^{r-t}}{t!\,(52-2n)!\,2^{t+n-r}}\end{displaymath}

as the number of deals in which some subset of precisely 2t people get a pair of the same rank as someone else. We then sum this over t in the range mentioned above. This yields an expression for M(r).

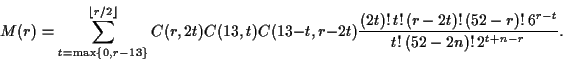
\begin{displaymath}M(r)=\sum_{t=\mathrm{max}\{0,r-13\}}^{\lfloor r/2\rfloor}C(r,... ...2t)!\,t!\,(r-2t)!\,(52-r)!\,6^{r-t}} {t!\,(52-2n)!\,2^{t+n-r}}.\end{displaymath}

We substitute this for M(r) in the above answer for the question and simplify. This yields

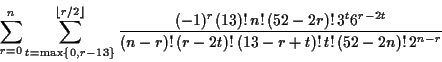
\begin{displaymath}\sum_{r=0}^n\sum_{t=\mathrm{max}\{0,r-13\}}^{\lfloor r/2\rflo... ...3^t6^{r-2t}}{(n-r)!\,(r-2t)!\,(13-r+t)!\,t!\,(52-2n)!\,2^{n-r}}\end{displaymath}

as the answer to the basic question of the number of ways in which two cards can be dealt to each of two people so that no one receives a pair. In order to compute the probability of such a deal occurring, simply divide the preceding number by the number of 2-card hands that can be dealt to n people which, as we saw earlier, is $(52)!/(52-2n)!\,2^n$.

In fact, with a little extra effort one can use the numbers obtained in the main formula to do much more. Let's illustrate with n=4. Using the formula one obtains M(0) = 1,896,396,138,000 which is the total number of ways of dealing two cards to each of four players. Continuing one obtains M(1) = 446,210,856,000, M(2) = 39,885,786,720, M(3) = 1,604,266,560, and M(4) = 24,480,144. The number M(4) is the number of deals in which all four players receive a pair.

Suppose we would like to know the probability of precisely three players being dealt a pair. The number M(3) is the number of deals in which three players receive a pair. However, for each of the C(4,3) = 4subsets of three properties, we also are including the number of deals in which all four players receive a pair. Therefore, we must subtract 4M(4) from M(3) to obtain the number of deals in which precisely three players receives a pair. This yields 1,506,345,984 deals (we essentially are doing inclusion-exclusion with the 3-subsets as our base set) for which precisely three players receive pairs.

Let's now do the same for a subset of two players. Once this example is understood the process should be clear. First, there are C(4,2) = 6 subsets with two players each. Now M(2) gives us the total number of deals for which the subsets of two players are dealt pairs. As before, this includes deals with pairs going to three and four players. There are two 3-subsets containing a given 2-subset and there is the single 4-set containing it. This means we have a contribution from 12 3-subsets (obtained from $6\cdot 2$) which must be subtracted. Since M(3) includes deals for four 3-subsets, we subtract 12/4 = 3 times M(3). The 4-subset is counted six times in M(2) and four times in M(3). Thus, it is counted negative six times in M(2)-3M(3). So we must add 6M(4) in order to have deals with all four players receiving a pair contributing zero to the count. This gives us M(2)-3M(3)+6M(4) = 35,219,867,904 deals in which precisely two players are dealt a pair. (Again it is inclusion-exclusion with the 2-subsets as the base set.)

The preceding technique allows us easily to obtain the following table of probabilities. The columns correspond to the exact number of players receiving a pair and the rows correspond to the number of players being dealt. For example, the probability exactly one player is dealt a pair when dealing to four people is .196. A blank entry means an entry is inappropriate and a neg entry means the probability is so small it is negligible.


  0 1 2 3 4 5 6 7 8 9 10 11
1 .941 .059                    
2 .886 .111 .0035                  
3 .834 .156 .0099 .0002                
4 .785 .196 .019 .0008 neg              
5 .739 .230 .029 .0019 .0001 neg            
6 .700 .259 .042 .0032 .0003 neg neg          
7 .655 .285 .054 .0058 .0004 neg neg neg        
8 .617 .306 .068 .0086 .0007 neg neg neg neg      
9 .581 .324 .082 .012 .0012 .0001 neg neg neg neg    
10 .547 .339 .096 .016 .0019 .0001 neg neg neg neg neg  
11 .515 .351 .110 .021 .0027 .0003 neg neg neg neg neg neg


Home | Publications | Preprints | MITACS | Poker Digest | Poker Computations | Feedback
website by the Centre for Systems Science
last updated 27 August 2001