Expectations Galore: Bad Bets

On a recent trip through Vancouver I ran into Bib Ladder at one of the local cardrooms. After exchanging introductory pleasantries, we got into a discussion about what the worst bet in a casino might be.

``Well, professor, I understand keno is a game with considerable return for the house,'' said Bib. ``True, but recently I calculated the player's expectation and it turns out the house is returning between 71 to 79 percent which is bad but not as bad as some others.''

Bib replied, ``I was just reading this book here entitled Gambling Like a Pro by Stanford Wong and Susan Spector in which they state someone named Stanley Ko claims the bonus bet return in Let It Ride is only in the neighborhood of 45 cents on the dollar. These two authors are highly reliable and 45 cents on the dollar sounds like a good bet for worst bet in the house to me.''

``Alright, Bib, let's take a look at the bonus bet in Let It Ride. Furthermore, let's use the bonus payout schedule right here on page 197.

Calculating the expectation for this bet is straightforward. We simply take the probability of achieving each of the winning hands, multiply by the payoff and add them together to get the expectation.

Altogether there are C(52,5) = 2,598,960 five-card poker hands. We have never counted the various five-card poker hands before so let's quickly run through the numbers. There are four royal flushes. There are 36 non-royal straight flushes by considering what the smallest cards may be. There are 13 choices for the ranks of a 4-of-a-kind and 48 remaining cards. The product of the two yields 624 4-of-a-kinds.

For a full house, there are 13 choices for the rank of the triple and 12 choices for the rank of the pair. There are four ways of choosing the triple and six ways of choosing the pair. The product of these numbers produces 3,744 full houses.

There are four choices for the suit of a flush and C(13,5) = 1,287choices for the five cards in the suit. The product is 5,148, but we must remove the 40 straight flushes giving us 5,108 flushes. To count straights, we observe there are ten rank sequences of the form x,x+1,x+2,x+3,x+4 corresponding to a straight. There are four choices for each of the cards of the different ranks giving 4⁵ = 1,024ways to fill in the straight. Multiplying by 10 and subtracting the 40 straight flushes yields 10,200 straights.

For three-of-a-kind, there are 13 choices for the rank of the trips, C(12,2) = 66 choices for the other two ranks, four choices for the trips, and four choices for each of the cards of the latter ranks. Multiplying this out produces 54,912 3-of-a-kind hands.

For two pair there are C(13,2) = 78 choices for the ranks of the pairs, 11 choices for the rank of the remaining card, six choices for each of the pairs, and four choices for the remaining card. The product is 123,552 which is the number of two pair hands.

The number of remaining hands is 2,400,780 and the bonus bet is lost for all these hands.

The payout schedule we are using is as: $20,000 for a royal flush; $2,000 for a non-royal straight flush; $100 for four-of-a-kind; $75 for a full house; $50 for a flush; $25 for a straight; $9 for three-of-a-kind; and $6 for two pair. Now we calculate the expectation -- remembering our profit is diminished by one because the bonus bet has already been collected. Everything is divided by 2,598,960 at the end since each of the probabilities is obtained by dividing by the total number of five-card hands. Thus, the numerator in the expectation calculation is given by

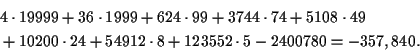
``Now wait a minute there, professor. That is in sharp disagreement with the book.''

``I don't understand it either, Bib. Perhaps Mr. Ko was making an adjustment for the limitation imposed by a maximum aggragate payout which some tables have in place. For example, if there is a maximum of $25,000 for the aggragate payout and a player had $10 on each of three bets, then should he get a royal flush, he would be paid $25,000 and receive nothing additional for the bonus bet. But even this reduces the expectation by only 79,996 in the numerator accounting for a decrease of only .031 in the bonus bet expectation.

Perhaps the disagreement is accounted for by poor wording in the book you have in your hands. You should look at the bonus bet as a side bet and as a side bet it is returning slightly more than 86 cents on the dollar. We'll have to look elsewhere for the worst bet in a casino.''

Various casinos have made adjustments in the payouts for the bonus bet in Let It Ride. In some cases the bet does become a candidate for worst bet in the casino. If you wish to work out the expectation for yourself, substitute the correct profit in the above formula, perform the arithmetic and divide by 2,598,960. I've seen a few casinos which pay for a pair of 10s or better for the bonus bet. In this case, multiply the profit for a pair of tens or better by 422,400 (the number of ways of getting a pair of 10s or better) and reduce the negative term from -2,400,780 to -1,978,380.