In this section, we prove Thereom 1.2, that is, we are interested in
decomposing the complete graph Kn into cycles of length m when
m and n are odd positive integers and
![]() .
As in Section 3, we begin by presenting the way in which
we wish to view the graph Kn.
.
As in Section 3, we begin by presenting the way in which
we wish to view the graph Kn.
The preceding definition implies that the graph Kn can be viewed as
the join of a circulant graph of order n - 1 with K1, that is,
Kn
= H(n;A) where
![]() .
.
PROOF.Label the vertices of the subcirculant with
![]() .
We
have
.
We
have
![]() if and only if
if and only if
![]() .
Let
.
Let
![]() denote the permutation
denote the permutation
![]() .
If L is
any subgraph of H(n;A), then
.
If L is
any subgraph of H(n;A), then ![]() is defined as
is defined as
![]() .
.
Let P be the trail of length
![]() given by
given by
Let w denote the last vertex of P, that is,
We now present the proof of our second main result.
PROOF OF THEOREM 1.2. Let m and n be positive odd integers
with
![]() .
Recall that by a result given
in [7], it
is sufficient to prove the theorem for values of m and n with
.
Recall that by a result given
in [7], it
is sufficient to prove the theorem for values of m and n with
![]() .
Thus, we may write n as n = m+r or n = 2m+rwhere
.
Thus, we may write n as n = m+r or n = 2m+rwhere
![]() .
Let
.
Let
![]() and label the
vertices of the graph H(n;A) with
and label the
vertices of the graph H(n;A) with
![]() ,
where u is the vertex of K1 (see Definition 4.1). Let
,
where u is the vertex of K1 (see Definition 4.1). Let
![]() denote the permutation
denote the permutation
![]() .
There
are two cases depending on whether n = m + r or n = 2m+r.
.
There
are two cases depending on whether n = m + r or n = 2m+r.
CASE 1. SUPPOSE THAT N = M+R. Clearly, if r=0, we
are done by the Walecki Hamilton decomposition of Kn found in [9].
Thus, we may assume that 0<r<m. Suppose B is a subset of A such
that |B| =r/2 and that we can decompose the circulant
![]() into m-cycles. Since
into m-cycles. Since
![]() and
since H(n;A-B) can be decomposed into m-cycles by
Lemma 4.2, we have a decomposition of H(n;A) into
m-cycles. Thus, our goal is to choose a convenient set B of r/2lengths. Since m and n are odd, it must be that r is even, say
r = 2ea, with a odd. Since
and
since H(n;A-B) can be decomposed into m-cycles by
Lemma 4.2, we have a decomposition of H(n;A) into
m-cycles. Thus, our goal is to choose a convenient set B of r/2lengths. Since m and n are odd, it must be that r is even, say
r = 2ea, with a odd. Since
![]() ,
we
also have that
,
we
also have that
![]() .
Since
r(r-1)/2=
2e-1a(2ea-1), we may write m as m = a'b' where
.
Since
r(r-1)/2=
2e-1a(2ea-1), we may write m as m = a'b' where ![]() and
and
![]() .
Let r/2 = a'c.
Next,
.
Let r/2 = a'c.
Next,
When a'=3, let
If c > 1, then, for each
For
If
In this case, b'=r-1 and if we express b' in the form b'=a't+s,
Let us examine the lengths of various linking edges arising from arcs
of Hamilton directed cycles resulting from the circulant graphs. If we
have an arc from vi to vk, then we would be joining the terminal
vertex of some Pj,i to the initial vertex of Pj,k. The length
of such a linking edges is
SUBCASE 1.2. SUPPOSE THAT
If c = 4q, then
There is so much latitude that the other cases are easy to do too.
For example, if c=4q+1, use the sets of paths
Finally, suppose that
If c > 1, then, for each
Let
CASE 2. SUPPOSE THAT
Thus, we may assume that r>1. To complete the proof we extend the
method used to solve the preceding case in which r=1. We note that
this means the proof will be different from all previous cases because
we no longer can build two diametrically opposed symmetric paths which
are linked to form a cycle via one or two central vertices. Instead, we
now use (r-1)/2 lengths to generate m-cyles by breaking the nvertices into segments, and we use the remaining m lengths to form
a single m-cycle which is acted on by
Let r=2ea+1, a'|a,
b'|(2ea+1), m=a'b' and m>r. Then
n=2m+r=b'(2a'+(2ea+1)/b'). Chop the vertices into b' segments
each having
2a'+(2ea+1)/b' vertices. Let
c=(r-1)/2a'=2e-1a/a'.
We have
Write c in the form
We are going to use edges whose lengths are congruent to
In the special case that a'=3, we use
P0,0=u0,u2,u-1 and
P1,0=u0,u4,u-1.
Let P2j,0 be obtained by adding
Let us verify that all the lengths employed are distinct. The length
of the longest edge is
We now show that we can use the remaining m lengths to form an
m-cycle. Arrange the remaining lengths in ascending order
This leaves us with the problem of what to do when
Notice that
If c=4k+1, we link the paths of
For c=4k+2, we link the paths of
This leaves us with the case that (a'-1)/2 is even. It is rather
similar to the case when (a'-1)/2 is odd so that we outline how to do it.
Let
SUBCASE 1.1. SUPPOSE THAT
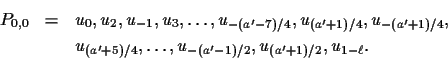
Observe that the lengths of the edges of P0,0 are
![]() .
Obtain the path P0,1 as before, that is,
.
Obtain the path P0,1 as before, that is,
![]() .
Since
.
Since
![]() ,
the paths P0,0 and
P0,1 are vertex-disjoint. Again, let the powers of
,
the paths P0,0 and
P0,1 are vertex-disjoint. Again, let the powers of ![]() act
on P0,0 to obtain the paths P0,0, P0,1,
act
on P0,0 to obtain the paths P0,0, P0,1, ![]() ,
P0, b'-1. Let
,
P0, b'-1. Let
![]() .
.
![]() ,
and when a'=7, let
,
and when a'=7, let
![]() .
.
![]() ,
obtain the path
Pj,0 from P0,0 by adding
,
obtain the path
Pj,0 from P0,0 by adding ![]() to the subscripts of the
even vertices of P0,0, that is,
to the subscripts of the
even vertices of P0,0, that is,
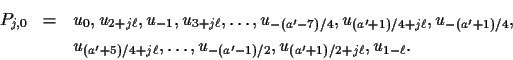
and continue as before letting the powers of ![]() act on Pj,0.
Then the lengths of the edges of the paths are
act on Pj,0.
Then the lengths of the edges of the paths are
![]() .
.
![]() ,
let
,
let
![]() denote the collection of paths
Pj,0, Pj,1,
denote the collection of paths
Pj,0, Pj,1, ![]() ,
Pj,b'-1. Then the set
,
Pj,b'-1. Then the set
![]() consists of c(a'-1) lengths.
Also, the longest edge of
consists of c(a'-1) lengths.
Also, the longest edge of
![]() has
length
has
length
![]() ,
and it is easy to see that
,
and it is easy to see that
![]() .
Note also that
.
Note also that
![]() contains no length that is congruent to
contains no length that is congruent to ![]() modulo
modulo ![]() as long as
as long as
![]() (we handle this case separately). Thus, we may use
circulants of order b' to link each family
(we handle this case separately). Thus, we may use
circulants of order b' to link each family
![]() into an
m-cycle Cj as in Subcase 2.2
of the proof of Theorem 1.1. Then the collection
into an
m-cycle Cj as in Subcase 2.2
of the proof of Theorem 1.1. Then the collection
![]()
is a partition of the edge set of the circulant H into m-cycles.
![]() and a'>3, let
and a'>3, let
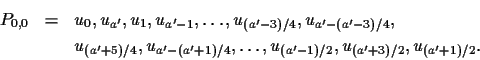
For a'=3, let
P0,0=u0,u3,u2. The lengths used are
![]() .
Let the other paths in
.
Let the other paths in
![]() be obtained exactly as above. We use
circulants of order b' for linking the families of paths into m-cycles.
The difference now is that the linking edges have lengths congruent to
be obtained exactly as above. We use
circulants of order b' for linking the families of paths into m-cycles.
The difference now is that the linking edges have lengths congruent to
![]() modulo
modulo ![]() .
We must be careful because -(a'+1)/2is congruent to (a'+1)/2 modulo
.
We must be careful because -(a'+1)/2is congruent to (a'+1)/2 modulo ![]() .
.
![]() ,
we find that a'b'=m divides the number of edges in
Km+r if and only if s=a'-1. Since m is odd, t must be odd.
Thus, r=a'(t+1) so that
b'=a'(t+1)-1 and c=(t+1)/2.
,
we find that a'b'=m divides the number of edges in
Km+r if and only if s=a'-1. Since m is odd, t must be odd.
Thus, r=a'(t+1) so that
b'=a'(t+1)-1 and c=(t+1)/2.
![]() .
If the arc goes from
vk to vi, then the length of the linking edge is
.
If the arc goes from
vk to vi, then the length of the linking edge is
![]() .
So if c=4q, then we use Hamilton decompositions of the
degree 4 circulants
.
So if c=4q, then we use Hamilton decompositions of the
degree 4 circulants
![]() as before. Since
as before. Since
![]() ,
the lengths of the linking edges are smaller than (n-1)/2.
Similar arguments work for c=4q+1, c=4q+2 and c=4q+3.
,
the lengths of the linking edges are smaller than (n-1)/2.
Similar arguments work for c=4q+1, c=4q+2 and c=4q+3.
![]() .
First, suppose that
.
First, suppose that
![]() .
As in the case
.
As in the case ![]() of subcase
1.1, we obtain
b'=a'(t+1)-1, c=(t+1)/2 and t is odd. Let
of subcase
1.1, we obtain
b'=a'(t+1)-1, c=(t+1)/2 and t is odd. Let
![]()
Obtain the paths
![]() .
by letting powers of
.
by letting powers of ![]() act on P0,0 in the usual way.
For each j satisfying j>0, obtain Pj,0 by adding
act on P0,0 in the usual way.
For each j satisfying j>0, obtain Pj,0 by adding ![]() to the
subscripts of all the even vertices of P0,0. Then obtain
to the
subscripts of all the even vertices of P0,0. Then obtain
![]() from Pj,0 by letting powers of
from Pj,0 by letting powers of ![]() act
on it. Let
act
on it. Let
![]() denote the family of paths
denote the family of paths
![]() .
.
![]() .
Use the sets of paths
.
Use the sets of paths
![]() .
Note that the longest edge has
length
.
Note that the longest edge has
length
![]() .
We use Hamilton directed cycles arising from
Hamilton decompositions of
.
We use Hamilton directed cycles arising from
Hamilton decompositions of
![]() ,
,
![]() ,...,
,...,
![]() .
These linking edges have length longer than
.
These linking edges have length longer than
![]() and less
than (n-1)/2 so that all lengths are distinct.
and less
than (n-1)/2 so that all lengths are distinct.
![]() ,
the same linking scheme for 4q of the
families, and edges of length (a'+3)/2 to link together the other
family. The cases c=4q+2 and c=4q+3 can be done similarly.
,
the same linking scheme for 4q of the
families, and edges of length (a'+3)/2 to link together the other
family. The cases c=4q+2 and c=4q+3 can be done similarly.
![]() .
Let
.
Let
![]() and note that t is odd. Consider the walk P0,0 of length a'-1defined by
and note that t is odd. Consider the walk P0,0 of length a'-1defined by
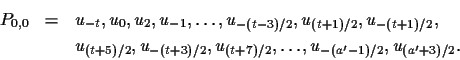
Since
t > (a'+2) - (a'+1)/2 - 2 = (a'-1)/2, we have that P0,0 is
a path. When t=3 and a'=5, the preceding path is
P0,0=u-3,
u0,u2,u-2,u4. Continue as in Case 1, letting the powers of
![]() act on P0,0 to obtain the paths
act on P0,0 to obtain the paths
![]() .
Observe that
.
Observe that
![]() so that these paths are
vertex-disjoint. Join the last vertex of P0,i to the first vertex
of P0,i+1 for
so that these paths are
vertex-disjoint. Join the last vertex of P0,i to the first vertex
of P0,i+1 for
![]() ,
and join the last vertex of
P0,b'-1 to the first vertex of P0,0 to form the m-cycle C0.
The lengths of the edges of C0 are the elements of the set
,
and join the last vertex of
P0,b'-1 to the first vertex of P0,0 to form the m-cycle C0.
The lengths of the edges of C0 are the elements of the set
![]() .
.
![]() ,
obtain the path
Pj,0 from P0,0 by subtracting
,
obtain the path
Pj,0 from P0,0 by subtracting ![]() from the subscript of
the first vertex and adding
from the subscript of
the first vertex and adding ![]() to the subscripts of the remaining
odd vertices of P0,0, that is,
to the subscripts of the remaining
odd vertices of P0,0, that is,
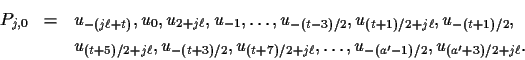
and continue as before letting the powers of ![]() act on Pj,0.
Join the last vertex of Pj,i to the first vertex of Pj,i+1 for
act on Pj,0.
Join the last vertex of Pj,i to the first vertex of Pj,i+1 for
![]() and join the last vertex of
Pj,b'-1 to the first
vertex of Pj,0 to form the m-cycle Cj. Note that these edges
all have length
and join the last vertex of
Pj,b'-1 to the first
vertex of Pj,0 to form the m-cycle Cj. Note that these edges
all have length ![]() .
Thus the lengths of the edges of Cj are
the elements of the set
.
Thus the lengths of the edges of Cj are
the elements of the set
![]() .
.
![]() .
Then the longest edge
of B has length
.
Then the longest edge
of B has length
![]() or
or
![]() .
We already
have seen that
.
We already
have seen that
![]() and it is not hard also to see
that
and it is not hard also to see
that
![]() .
Thus B consists of r/2 distinct
lengths. Therefore, the collection
.
Thus B consists of r/2 distinct
lengths. Therefore, the collection
![]()
is a partition of the edge set of the circulant
![]() into m-cycles.
into m-cycles.
![]() ,
the length of the edge uiuj is either i - j or j - i,
depending on which lies between 1 and (n-1)/2 modulo n. Let
,
the length of the edge uiuj is either i - j or j - i,
depending on which lies between 1 and (n-1)/2 modulo n. Let
![]() .
Next, suppose that
(m-1)/2 is odd. Consider the m-cycle C given by
.
Next, suppose that
(m-1)/2 is odd. Consider the m-cycle C given by
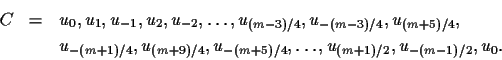
Then
![]() is a partition of
the edge set of Kn into m-cycles. Now suppose that (m-1)/2 is
even. Consider the m-cycle C given by
is a partition of
the edge set of Kn into m-cycles. Now suppose that (m-1)/2 is
even. Consider the m-cycle C given by
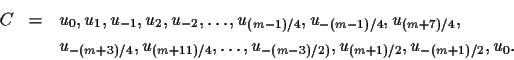
As before,
![]() is a partition
of the edge set of Kn into m-cycles. Therefore, the graph K2m+1can be decomposed into m-cycles.
is a partition
of the edge set of Kn into m-cycles. Therefore, the graph K2m+1can be decomposed into m-cycles.
![]() .
.
![]()
giving us a lower bound on the number of segments.
![]() .
Suppose t=0 and
(a'-1)/2 is odd. Let
.
Suppose t=0 and
(a'-1)/2 is odd. Let
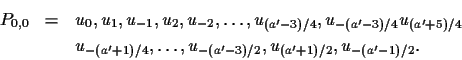
The lengths of the edges of P0,0 are
![]() .
Obtain
.
Obtain
![]() in the usual way
by letting powers of
in the usual way
by letting powers of ![]() act on P0,0.
act on P0,0.
![]() modulo
modulo ![]() as linking edges to form cycles. Thus, in forming P1,0we do not want to use an edge of length
as linking edges to form cycles. Thus, in forming P1,0we do not want to use an edge of length
![]() .
Let P be the
path obtained from P0,0 by adding a' to the subscripts
of all even vertices of P0,0. The lengths of the edges used in Pare
.
Let P be the
path obtained from P0,0 by adding a' to the subscripts
of all even vertices of P0,0. The lengths of the edges used in Pare
![]() .
If
.
If
![]() ,
then let P1,0=P. If
,
then let P1,0=P. If
![]() ,
then
in P do not omit the vertex
ua'+(a'+1)/4; instead, omit the
vertex which would lead to the edge of length
,
then
in P do not omit the vertex
ua'+(a'+1)/4; instead, omit the
vertex which would lead to the edge of length
![]() being
omitted. Since
being
omitted. Since
![]() is even, the omitted vertex is in the
interval from u0 to
is even, the omitted vertex is in the
interval from u0 to ![]() and the last vertex in the interval
from u0 to
and the last vertex in the interval
from u0 to ![]() in the resulting path still is
ua'+(a'+1)/2. This is the path P1,0. Now
obtain
in the resulting path still is
ua'+(a'+1)/2. This is the path P1,0. Now
obtain
![]() from P1,0 using powers
of
from P1,0 using powers
of ![]() again. Observe that the paths
again. Observe that the paths
![]() are mutually vertex-disjoint because
are mutually vertex-disjoint because ![]() implies
implies
![]() .
.
![]() to the subscripts of the
even vertices of P0,0, and obtain
to the subscripts of the
even vertices of P0,0, and obtain
![]() from
P2j,0 in the usual way. Finally, obtain
P2j+1,0 by adding
from
P2j,0 in the usual way. Finally, obtain
P2j+1,0 by adding ![]() to the subscripts of the even vertices of P1,0, and obtain
to the subscripts of the even vertices of P1,0, and obtain
![]() as before. Let
as before. Let
![]() .
None of the paths use edges whose lengths are
congruent to
.
None of the paths use edges whose lengths are
congruent to
![]() modulo
modulo ![]() .
We use edges of these lengths
to link the paths of
.
We use edges of these lengths
to link the paths of
![]() together to form m-cycles based on
Hamilton directed cycles arising from Hamilton decompositions of
circulants of order b' and degree 4 as done for earlier cases. Use
the circulant
together to form m-cycles based on
Hamilton directed cycles arising from Hamilton decompositions of
circulants of order b' and degree 4 as done for earlier cases. Use
the circulant
![]() for the collection of paths
for the collection of paths
![]() and
and
![]() ,
,
![]() .
.
![]() ,
and the number of vertices
is
,
and the number of vertices
is
![]() .
Thus, all edge lengths are distinct.
.
Thus, all edge lengths are distinct.
![]() .
Since the longest length already used is
.
Since the longest length already used is
![]() and (r-1)/2 lengths have been used, the lengths
and (r-1)/2 lengths have been used, the lengths
![]() consist of successive integers from
consist of successive integers from
![]() through (n-1)/2, where
through (n-1)/2, where
![]() .
Start a path P according to
.
Start a path P according to
![]()
noting that s is odd. All lengths
![]() are used in P. Let
are used in P. Let
![]() so
that the terminal vertex of P is distance x from u0. We know
that
so
that the terminal vertex of P is distance x from u0. We know
that
![]() is even and that the remaining
lengths are successive integers. We shall complete P to a path P'of length m-2 by continuing in the form
is even and that the remaining
lengths are successive integers. We shall complete P to a path P'of length m-2 by continuing in the form
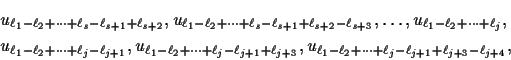
and so on until reaching
![]() .
Notice that P' has been
obtained by successively zigzagging with edges of increasing length and
omitting one edge of odd length
.
Notice that P' has been
obtained by successively zigzagging with edges of increasing length and
omitting one edge of odd length
![]() .
Let u-z be the
vertex immediately preceding uy in P'. If we wish to add an edge
of length (n-1)/2 to P', it will go from uy to either u-z-1or u-z-2. Let w be the odd integer amongst z+1 and z+2. If
.
Let u-z be the
vertex immediately preceding uy in P'. If we wish to add an edge
of length (n-1)/2 to P', it will go from uy to either u-z-1or u-z-2. Let w be the odd integer amongst z+1 and z+2. If
![]() ,
then let w be the odd length
,
then let w be the odd length
![]() omitted to form P'. Adding the 2-path
uy,u-w,u0 to P' yields
an m-cycle C' using all of the missing lengths precisely once.
Letting
omitted to form P'. Adding the 2-path
uy,u-w,u0 to P' yields
an m-cycle C' using all of the missing lengths precisely once.
Letting ![]() act on C' completes the decomposition.
act on C' completes the decomposition.
![]() .
The first step is to let
.
The first step is to let
![]() be the odd length
edge we delete in forming P'.
Currently, P' ends with
uy-1,u-z,uy, the edge
uy-1u-zhas length (n-5)/2, and the edge u-zuy has length (n-3)/2.
Perform the following alteration of P'. From uy-1 reverse the
order of the lengths encountered to (n-1)/2, (n-3)/2, (n-5)/2and since there are two choices for the edge of length (n-1)/2, the
altered path terminates at either u-z-3 or u-z-4. If either
z+3 or z+4 equals
be the odd length
edge we delete in forming P'.
Currently, P' ends with
uy-1,u-z,uy, the edge
uy-1u-zhas length (n-5)/2, and the edge u-zuy has length (n-3)/2.
Perform the following alteration of P'. From uy-1 reverse the
order of the lengths encountered to (n-1)/2, (n-3)/2, (n-5)/2and since there are two choices for the edge of length (n-1)/2, the
altered path terminates at either u-z-3 or u-z-4. If either
z+3 or z+4 equals
![]() ,
then we close the path to an
m-cycle with an edge of length
,
then we close the path to an
m-cycle with an edge of length
![]() .
If
.
If
![]() ,
then start the alteration of P' at uy-2.
It is then possible to have the altered path terminate at either
u-z-5 or u-z-6. If either z+5 or z+6 equals
,
then start the alteration of P' at uy-2.
It is then possible to have the altered path terminate at either
u-z-5 or u-z-6. If either z+5 or z+6 equals
![]() ,
then we complete to an m-cycle as before. We need to show
we can achieve an alteration of P' so that it terminates at
,
then we complete to an m-cycle as before. We need to show
we can achieve an alteration of P' so that it terminates at
![]() .
We have
.
We have
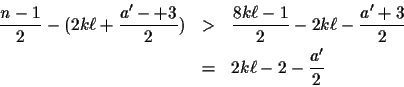
edges whose lengths are consecutive integers from
![]() through (n-1)/2. We wish to show the longest subpath which would need
to be reversed so that P' terminates at
through (n-1)/2. We wish to show the longest subpath which would need
to be reversed so that P' terminates at
![]() has
length less than
has
length less than
![]()
![]() implies
implies
![]() are successive integers in the sequence
are successive integers in the sequence
![]() .
This in turn implies a gap of length at least (a'+3)/2in the vertices having negative subscripts when forming the m-cycle.
On the other hand, when
.
This in turn implies a gap of length at least (a'+3)/2in the vertices having negative subscripts when forming the m-cycle.
On the other hand, when
![]() ,
we have
,
we have
![]() and
and
![]() .
Thus, the first vertex employed in
the m-cycle which has a negative subscript is
u-(a'+3)/2. In
either case, it is easy to see that
.
Thus, the first vertex employed in
the m-cycle which has a negative subscript is
u-(a'+3)/2. In
either case, it is easy to see that
![]()
using the facts m>n/3 and ![]() .
Since
.
Since
![]()
the longest subpath which would need to be reversed has length less
than
![]() .
Observe that
.
Observe that
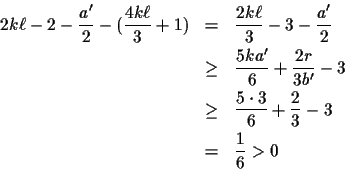
because ![]() ,
,
![]() and b'|r. (When k=0 the previous
case applies.) So there is a sufficiently long sequence of consecutive
edge lengths available for reversing a subpath to allow us to form an
m-cycle.
and b'|r. (When k=0 the previous
case applies.) So there is a sufficiently long sequence of consecutive
edge lengths available for reversing a subpath to allow us to form an
m-cycle.
![]() to form an m-cycle
using edges of length
to form an m-cycle
using edges of length
![]() .
We then use Hamilton
decompositions of
.
We then use Hamilton
decompositions of ![]()
to handle the families
![]() .
The remaining m lengths are handled as in the previous case.
.
The remaining m lengths are handled as in the previous case.
![]() and
and
![]() to form two m-cycles using edges of lengths
to form two m-cycles using edges of lengths
![]() ,
respectively. The remaining families of paths and the resulting mlengths are done as before. Finally, for c=4k+3, use the lengths
,
respectively. The remaining families of paths and the resulting mlengths are done as before. Finally, for c=4k+3, use the lengths
![]() and
and
![]() to link the paths
to link the paths
![]() ,
,
![]() and
and
![]() ,
respectively. Use Hamilton decompositions
of
,
respectively. Use Hamilton decompositions
of ![]()
for
![]() .
The remaining m-lengths are
done as before.
.
The remaining m-lengths are
done as before.
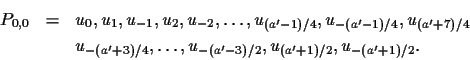
The path P0,0 uses edges of lengths
![]() .
One slight difference here is that the length a'has not been used. Thus, we start the path P1,0 as
u0,ua',
u-2 and note that the lengths of the first two edges are a' and
a'+2 neither of which appear amongst the lengths for P0,0. We
then continue the zigzag pattern as in P0,0 except that no more
vertices are omitted from the interval not containing u0 from
u-2 to
u-(a'+1)/2. This means that the path P1,0 also
terminates at
u(-a'+1)/2. This means that the lengths of the
connecting edges used to link families of paths together to form
m-cycles are congruent to
.
One slight difference here is that the length a'has not been used. Thus, we start the path P1,0 as
u0,ua',
u-2 and note that the lengths of the first two edges are a' and
a'+2 neither of which appear amongst the lengths for P0,0. We
then continue the zigzag pattern as in P0,0 except that no more
vertices are omitted from the interval not containing u0 from
u-2 to
u-(a'+1)/2. This means that the path P1,0 also
terminates at
u(-a'+1)/2. This means that the lengths of the
connecting edges used to link families of paths together to form
m-cycles are congruent to
![]() modulo
modulo ![]() .
Hence, we
want to make certain we do not use an edge with length
.
Hence, we
want to make certain we do not use an edge with length
![]() in P1,0. Since
in P1,0. Since
![]() is even, we can avoid using it by
shifting the vertices in the interval containing ua'+1 from
ua' to
ua'+(a'-3)/2 if
is even, we can avoid using it by
shifting the vertices in the interval containing ua'+1 from
ua' to
ua'+(a'-3)/2 if
![]() .
Otherwise,
we need shift no vertices in that interval. With these two starting
paths the argument is the same as the preceding case. This completes
the proof of Theorem 1.2.
.
Otherwise,
we need shift no vertices in that interval. With these two starting
paths the argument is the same as the preceding case. This completes
the proof of Theorem 1.2.
Brian &
2000-01-20