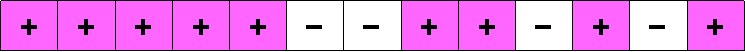
A length 13 Barker sequence.
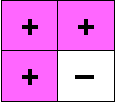
A 2×2 Barker array.
In communications engineering, an ideal binary sequence is a Barker sequence, for which all the out-of-phase aperiodic autocorrelations have magnitude at most 1. Although Barker sequences can easily be found for lengths 2, 3, 4, 5, 7, 11 and 13, there is overwhelming evidence that longer Barker sequences do not exist.
Given both the potential usefulness and the scarcity of Barker sequences, one practical option is to relax the Barker condition by seeking binary sequences whose aperiodic autocorrelations are collectively small, as measured by the merit factor or the peak sidelobe level. A second option is to seek two sequences whose aperiodic autocorrelations sum to zero in all out-of-phase positions, known as a pair of Golay complementary sequences. A third option is to generalise the Barker definition to multi-dimensional binary arrays. This was proposed by Alquaddoomi and Scholtz for two-dimensional arrays in 1989, but after theoretical analysis and computational search they conjectured that an s×t Barker array with s, t > 1 exists only when s=t=2.
In 1993, I found combinatorial restrictions on the possible sizes of an s×t Barker array when st is even and, with Sheelagh Lloyd and Miranda Mowbray, when st is odd. In 2006 Jim Davis, Ken Smith and I revisited the problem and found a complete proof of the two-dimensional Barker array conjecture using only elementary methods.
Soon afterwards, Matthew Parker and I found a short proof that the two-dimensional result implies there are no Barker arrays having more than two dimensions, as conjectured by Dymond in 1992.
In 2015, Jason Bell, Mahdad Khatirinejad, Kai-Uwe Schmidt and I combined combinatorial arguments and algebraic number theory to establish severe restrictions on the possible sizes of a 3-phase Barker array.
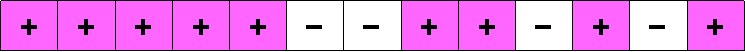
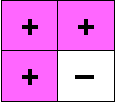
A 2×2 Barker array.