1. Industrial Mathematics

I am interested in modelling real problems from industry, primarily using partial differential equations (PDE) and then employing analytical and computational approaches to gain insight into their solution. My past and current projects in this area include:

1. Industrial problem-solving workshops (IPSWs): Also called study groups, these are workshops of approximately 4-5 days in length during which teams of academic problem-solvers attack problems of direct relevance to companies or other non-academic organizations. The International Study Groups Website has more information about these events and collects information about various industrial problem-solving workshops held around the world. I have been involved in a number of these workshops in the past, during which I've investigated land mine detection using the radon transform [C2], water flow in pipe networks [C3], and disease detection [C10].

   

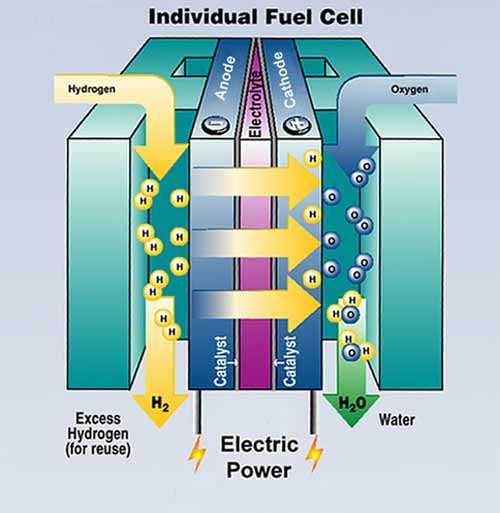
2. Hydrogen fuel cells: My main interests are in modelling and simulation of reactant transport in fuel cell electrodes [J9], [J10], [J17], [J18], [C6], [C7], [C9], and developing approximate analytical solutions for the underlying nonlinear PDEs [J8], [J12]. This work was carried over a period of 10 years as part of a multi-university project funded by grants from Mitacs. I am currently focusing my efforts on modelling of water-repellency in porous gas diffusion electrodes and multiscale aspects of catalyst layers.
   Industrial partner: Ballard Power Systems.

3. Biofilm growth and deformation: Biofilms are collections of microbial cells that grow on surfaces in moist, aqueous environments. We are interested in studying the interaction between the biofilm and a background fluid flow, incorporating effects of growth, deformation, attachment and detachment. Our aim is to use the immersed boundary method to simulate the fluid-structure interaction problem, along with a non-Newtonian fluid model that incorporates the biofilm properties in an averaged sense via a rheological constitutive law. This work arose from a collaborative research project funded by grants from Mitacs and the AFMNet Network of Centres of Excellence.
   Industrial partners: BioShield Technologies and Compass Group Canada
   

4. Pollutant transport in the atmosphere: We studied airborne zinc emissions from a large smelting operation, aiming to estimate emission rates based on ground-level deposition measurements. We incorporated an approximate solution to the advection-diffusion equation (known as the Gaussian plume solution) into a constrained least squares solver, and the resulting estimates were incorporated by our partner into their annual reporting to Environment Canada. This work has led to publications in both mathematical and applications journals [J40], [J39], [J37], [J16], [J20].
   Industrial partner: Teck Resources

5. Sap flow in maple trees.
   Industrial partner: North American Maple Syrup Council.

6. Traffic flow: We studied the flow of car and truck traffic on the South Fraser Perimeter Road connecting the DeltaPort container terminal with north Surrey. Both fluid dynamic and particle-hopping models are applied to gauge the impact of various design choices on the traffic flow within the region. These fluid dynamic models for traffic flow are closely related to some work I have already done related to hyperbolic conservation laws with discontinuous flux [J22] and modeling of multi-class traffic flow [M1].

7. Controlling robotic welding machines: I applied basic ideas from trigonometry and vector calculus to determine the parametric curve describing the path a robotic welding torch needs to follow when joining two cylindrical pipes of different cross-section. This work was written up as a paper in the Maple Technical Journal.
   Industrial partners: AIS Technologies and Zyco Manufacturing Ltd.

Below are a few more interesting links related to research in industrial mathematics:

• A nice general discussion of industrial mathematics can be found on the web page of my colleague, Randall Pyke.
• The report of the OECD Global Science Forum on Mathematics in Industry, a policy paper about the fundamental importance of mathematics in driving innovation in industry. I was actually a participant in the workshops during 2007-08 that led to this report.
• SIAM's Report on Mathematics in Industry (2012), which surveys the employment situation for nonacademic mathematicians as well as issues related to graduate training.