In this section, we prove Theorem 1.1, that is, we are interested in
proving that the graph Kn-I can be decomposed into
cycles of length m when m and n are even and
![]() .
The preliminaries have
been completed for the proof except for the
basic way in which we wish to view the graph Kn-I. We present this,
along with a lemma, and then proceed to the proof of the result.
.
The preliminaries have
been completed for the proof except for the
basic way in which we wish to view the graph Kn-I. We present this,
along with a lemma, and then proceed to the proof of the result.
The preceding definitions imply that the graph Kn - I can be thought
of as the join of a circulant
graph of order n - 2 with
![]() ,
that is,
Kn - I = H(n;A),
where
,
that is,
Kn - I = H(n;A),
where
![]() .
Thus the edges of length (n-2)/2in the circulant together with the edge uw make up the edges of the
1-factor I.
.
Thus the edges of length (n-2)/2in the circulant together with the edge uw make up the edges of the
1-factor I.
PROOF.Label the vertices of the subcirculant with
![]() .
We have
.
We have
![]() if and only if
if and only if ![]() .
Let
.
Let ![]() denote the permutation
denote the permutation
![]() .
If L is any subgraph of
H(n;A), then
.
If L is any subgraph of
H(n;A), then ![]() is defined as
is defined as
![]() .
.
Let P be the trail of length
![]() given by
given by
Thus, we can form a cycle C of length m by taking
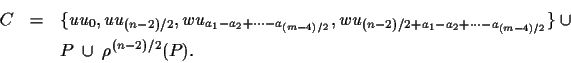
We now present the proof of the first main theorem.
PROOF OF THEOREM 1.1.
Let m and n be positive even integers with
![]() .
As mentioned in the introduction, if
n(n-2)/2 is an even multiple of m, then using [6,11] it is
not difficult to show that Kn - I can be decomposed into m-cycles.
To do so, we think of Kn-I as the wreath product
.
As mentioned in the introduction, if
n(n-2)/2 is an even multiple of m, then using [6,11] it is
not difficult to show that Kn - I can be decomposed into m-cycles.
To do so, we think of Kn-I as the wreath product
![]() ,
that is, replace every vertex of Kn/2 by a copy
of
,
that is, replace every vertex of Kn/2 by a copy
of
![]() and every edge of Kn/2 by a copy of K2,2.
A path P of length m/2 in Kn/2 becomes
and every edge of Kn/2 by a copy of K2,2.
A path P of length m/2 in Kn/2 becomes
![]() in Kn-I, and this graph can be decomposed into two cycles of length
m by the main result of [6]. The proof is completed by using
one of the main results of [11] to observe that Kn/2 can be
decomposed into paths of length m/2.
in Kn-I, and this graph can be decomposed into two cycles of length
m by the main result of [6]. The proof is completed by using
one of the main results of [11] to observe that Kn/2 can be
decomposed into paths of length m/2.
Because of the preceding paragraph, we may assume that n(n-2)/2 is
an odd multiple of m. Next, by Lemma 2.3, we may
also assume that n < 2m, say n=m+r for some positive integer
r with
![]() .
Now if r=0, we are done
by a construction of Walecki given in [9]. Thus, we assume
that 0 < r < m. We have
seen that
.
Now if r=0, we are done
by a construction of Walecki given in [9]. Thus, we assume
that 0 < r < m. We have
seen that
![]() implies that
implies that
![]() ,
and since n(n-2)/2 is an odd multiple of m,
Lemma 2.4 implies that r(r-2)/2 is an even multiple of m.
,
and since n(n-2)/2 is an odd multiple of m,
Lemma 2.4 implies that r(r-2)/2 is an even multiple of m.
Let
![]() and label the vertices of the graph
H(n;A) with
and label the vertices of the graph
H(n;A) with
![]() ,
where u and w are the
two vertices of
,
where u and w are the
two vertices of
![]() (see Definition 3.2).
Note that the edge joining ui and uj has length j-i or length
i-j depending on which lies between 1 and (n-2)/2 modulo n-2.
The proof of Theorem 1.1 proceeds as follows.
Suppose that B is a subset of A such that
(see Definition 3.2).
Note that the edge joining ui and uj has length j-i or length
i-j depending on which lies between 1 and (n-2)/2 modulo n-2.
The proof of Theorem 1.1 proceeds as follows.
Suppose that B is a subset of A such that
![]() ,
and
that we can decompose the circulant
,
and
that we can decompose the circulant
![]() into m-cycles.
Then since
into m-cycles.
Then since
![]() and
the graph H(n;A-B) can be decomposed into m-cycles by Lemma
3.4, it follows that we have a decomposition of H(n;A)into m-cycles. Thus, the rest of the proof consists of determining
a convenient set B of r/2 lengths such that the circulant
and
the graph H(n;A-B) can be decomposed into m-cycles by Lemma
3.4, it follows that we have a decomposition of H(n;A)into m-cycles. Thus, the rest of the proof consists of determining
a convenient set B of r/2 lengths such that the circulant
![]() can be decomposed into m-cycles.
can be decomposed into m-cycles.
By Lemma 2.4, we know that r is congruent to 0 or 2 modulo 8, and thus the proof now breaks into these two cases.
CASE 1. SUPPOSE THAT
Let
The definition of P0,0 does not make sense when
2d-2a'+2=1,
that is, d=2 and a'=1. In this case let
Let
b=r/(2d+1a') = 2e-d-1a/a'. If b > 1, then obtain the path
P1,0 by adding
Similarly, for each j with
For
CASE 2. SUPPOSE THAT
SUBCASE 2.1. SUPPOSE THAT
Since
Again, let the powers of
If b > 1, then obtain the path P1,0 from P0,0 by subtracting
Similarly, for
Let
SUBCASE 2.2. SUPPOSE THAT
There are two special cases that must be considered. When b'=7, let
If b > 1, then obtain the path P1,0 by adding
Similarly, for each j with
Recall that
There are several points we need to consider. First, if a Hamilton cycle
in G uses exactly one length for its edges, then it is easy to see that
it can be used to link together the paths of some
J.-C. Bermond, O. Favaron and M. Maheo [3] proved that any connected
circulant graph of degree 4 can be decomposed into two Hamilton cycles. So
we choose two lengths s1 and s2 in G such that
gcd
(s1,s2)=1, which guarantees that the circulant graph with connection
set
We now must show that there are enough edge-disjoint Hamilton cycles
in the auxiliary graph G to make the above scheme work. Recall that
the number of vertices in G is 2da' and that 2da'>2b.
We now proceed depending on the number of families
Finally, if b >3, then write
b = 4q + 1 or
b = 4q + 3 for some
positive integer q. Suppose first that
b = 4q + 1. Then
Upon obtaining all the m-cycles as described above, we then let
![]() .
Thus
r(r-2)/2=2ea(2e-1a-1). Since m divides r(r-2)/2 evenly,
we have that m=2da'b', where
.
Thus
r(r-2)/2=2ea(2e-1a-1). Since m divides r(r-2)/2 evenly,
we have that m=2da'b', where ![]() ,
,
![]() ,
and
,
and
![]() .
Then
.
Then
Partition the vertices of the circulant H into b' segments,
each with
![]() vertices. Each segment will
contribute 2da' edges to an m-cycle. Define the path P0,0 by
vertices. Each segment will
contribute 2da' edges to an m-cycle. Define the path P0,0 by
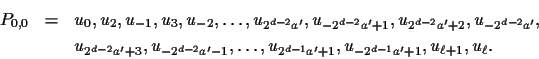
![]() ,
where
,
where ![]() is the permutation
from the proof of Lemma 3.4. Since
is the permutation
from the proof of Lemma 3.4. Since
![]() implies
that
implies
that
![]() ,
the vertices of P0,1 are
distinct from the vertices of P0,0 except for
,
the vertices of P0,1 are
distinct from the vertices of P0,0 except for ![]() ,
which is the
last vertex of P0,0 and the first vertex of P0,1. Similarly,
the paths
,
which is the
last vertex of P0,0 and the first vertex of P0,1. Similarly,
the paths ![]()
are vertex-disjoint except
that the path P0,i begins at the last vertex of P0,i-1 for
![]() and
P0,b'-1 ends at u0. Thus
and
P0,b'-1 ends at u0. Thus
![]() is an m-cycle
and the lengths of the edges of C0 are
is an m-cycle
and the lengths of the edges of C0 are
![]() .
.
![]()
![]() to the subscripts of the even vertices of
P0,0, that is,
to the subscripts of the even vertices of
P0,0, that is,
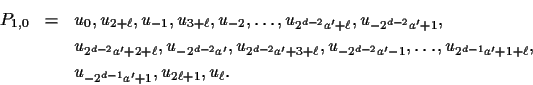
Next, obtain the paths
![]() by letting
powers of
by letting
powers of ![]() act on P1,0 in the same way they acted on P0,0.
Furthermore, the path
P1,i begins at the last vertex of
P1, i-1 for
act on P1,0 in the same way they acted on P0,0.
Furthermore, the path
P1,i begins at the last vertex of
P1, i-1 for
![]() and the last vertex of
P1,b'-1 is u0. Thus,
and the last vertex of
P1,b'-1 is u0. Thus,
![]() is an m-cycle, where the lengths of the edges of C1 are
is an m-cycle, where the lengths of the edges of C1 are
![]() .
.
![]() ,
obtain the path Pj,0 by
adding
,
obtain the path Pj,0 by
adding ![]() to the subcripts of the even vertices of P0,0.
Then the paths
to the subcripts of the even vertices of P0,0.
Then the paths
![]() are obtained
by letting powers of
are obtained
by letting powers of ![]() act on Pj,0.
Note here that Pj,i begins at the last vertex of Pj,i-1 for
act on Pj,0.
Note here that Pj,i begins at the last vertex of Pj,i-1 for
![]() and the last vertex of
Pj,b'-1 is u0.
Hence
and the last vertex of
Pj,b'-1 is u0.
Hence
![]() is an
m-cycle and the lengths of the edges of Cj are
is an
m-cycle and the lengths of the edges of Cj are
![]() .
.
![]() ,
let Bj denote the set of lengths that Cjuses, that is,
,
let Bj denote the set of lengths that Cjuses, that is,
![]() .
Let
.
Let
![]() .
Now the longest edge in B has length
.
Now the longest edge in B has length
![]() .
Since
2ea < 2da'b' implies that
.
Since
2ea < 2da'b' implies that
![]() ,
it
follows that
,
it
follows that
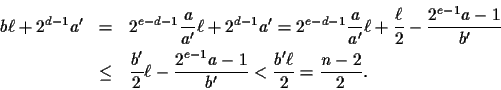
Therefore, the lengths of B are distinct and hence |B|=r/2.
Thus, the collection
![]()
is a partition of the edge set of the circulant
![]() into m-cycles.
into m-cycles.
![]() ,
,
![]() ,
and
,
and
![]() .
Let r/2=bb'. Then
.
Let r/2=bb'. Then
Let
![]() and note that
and note that
![]() .
The proof now breaks
into two subcases depending on the congruence class of b' modulo 4.
.
The proof now breaks
into two subcases depending on the congruence class of b' modulo 4.
![]() because b'=1 implies that
because b'=1 implies that
![]() which is a contradiction.
Let
which is a contradiction.
Let
![]() and note that s is odd. Consider the walk
P0,0 defined by
and note that s is odd. Consider the walk
P0,0 defined by
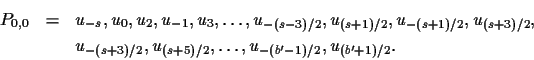
![]() ,
we have that the vertices of
P0,0 are distinct so that P0,0 is a path. In the case that
s=3, we have b'=5 and
,
we have that the vertices of
P0,0 are distinct so that P0,0 is a path. In the case that
s=3, we have b'=5 and ![]() ,
and
P0,0=u-3,u0,u2,u-2,u3.
Observe that the lengths of the edges of P0,0 are
,
and
P0,0=u-3,u0,u2,u-2,u3.
Observe that the lengths of the edges of P0,0 are
![]() .
Obtain the path P0,1 as before, that is,
.
Obtain the path P0,1 as before, that is,
![]() .
Since
.
Since
![]() ,
the paths P0,0 and
P0,1 are vertex-disjoint. Join the
first vertex of P0,1 to the last vertex of P0,0 and note that
this edge has length 1.
,
the paths P0,0 and
P0,1 are vertex-disjoint. Join the
first vertex of P0,1 to the last vertex of P0,0 and note that
this edge has length 1.
![]() act on P0,0 to obtain the paths
P0,0, P0,1,
act on P0,0 to obtain the paths
P0,0, P0,1, ![]() ,
P0, 2da'-1. Form the m-cycle C0by joining the last vertex of P0,i to the first vertex of P0,i+1for
,
P0, 2da'-1. Form the m-cycle C0by joining the last vertex of P0,i to the first vertex of P0,i+1for
![]() and joining the last vertex of
P0,2da'-1to the first vertex of P0,0.
Necessarily, these edges all have length 1. Let
and joining the last vertex of
P0,2da'-1to the first vertex of P0,0.
Necessarily, these edges all have length 1. Let
![]() .
.
![]() from the subscript of the first vertex and adding
from the subscript of the first vertex and adding ![]() to the
subscripts of the remaining odd vertices of P0,0, that is,
to the
subscripts of the remaining odd vertices of P0,0, that is,
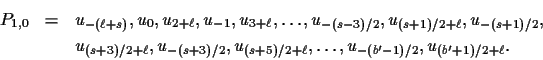
Then the lengths of the edges of P1,0 are
![]() .
As before, let the powers of
.
As before, let the powers of ![]() act on P1,0 to
obtain the paths
act on P1,0 to
obtain the paths
![]() .
Form the
m-cycle C1 by joining
the last vertex of P1,i to the first vertex of P1,i+1 for
.
Form the
m-cycle C1 by joining
the last vertex of P1,i to the first vertex of P1,i+1 for
![]() and joining the last vertex of
P1,2da'-1 to
the first vertex of P1,0. Note that these edges have length
and joining the last vertex of
P1,2da'-1 to
the first vertex of P1,0. Note that these edges have length ![]() .
.
![]() ,
obtain the path Pj,0 from P0,0by subtracting
,
obtain the path Pj,0 from P0,0by subtracting ![]() from the subscript of the first vertex and adding
from the subscript of the first vertex and adding
![]() to the subscripts of the remaining odd vertices of P0,0.
Again, letting the powers of
to the subscripts of the remaining odd vertices of P0,0.
Again, letting the powers of ![]() act on Pj,0, we form the m-cycle Cj by joining
the last vertex of Pj,i to the first vertex of Pj,i+1 for
act on Pj,0, we form the m-cycle Cj by joining
the last vertex of Pj,i to the first vertex of Pj,i+1 for
![]() and joining the last vertex of
Pj,2da'-1 to
the first vertex of Pj,0. Observe that these edges have length
and joining the last vertex of
Pj,2da'-1 to
the first vertex of Pj,0. Observe that these edges have length
![]() and thus the cycle Cj has edges with
lengths
and thus the cycle Cj has edges with
lengths
![]() .
.
![]() for
for
![]() ,
and let
,
and let
![]() Then the longest edge of B has length either
Then the longest edge of B has length either
![]() or
or
![]() .
Now r= 2bb' and
m = 2da'b', and since r < m, we have that
2b< 2da'. Thus,
.
Now r= 2bb' and
m = 2da'b', and since r < m, we have that
2b< 2da'. Thus,
![]() .
Therefore, the lengths
.
Therefore, the lengths
![]() are all distinct. Next,
are all distinct. Next,
![]()
so that B consists of r/2 distinct lengths. Hence, the collection
![]()
is a partition of the edge set of the circulant
![]() into m-cycles.
into m-cycles.
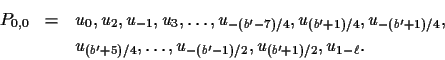
Note that P0,0 uses exactly one edge of each length
![]() and uses no edge whose
length is congruent to
and uses no edge whose
length is congruent to ![]() modulo
modulo ![]() .
Consider the paths
.
Consider the paths
![]()
and note that P0,i begins at vertex ![]() and ends at
and ends at
![]() .
.
![]()
When b'=3, the condition
m>r=2ea+2 forces a'=a and d=e-1 which
in turn implies ![]() .
The initial path
P0,0=u0,u3,u-4 works
in this case.
.
The initial path
P0,0=u0,u3,u-4 works
in this case.
![]() to the
subscripts of the even vertices of P0,0, that is,
to the
subscripts of the even vertices of P0,0, that is,
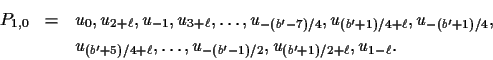
Next, obtain the paths
![]() by
letting powers of
by
letting powers of ![]() act on P1,0 as before. Observe that
these paths use edges of lengths
act on P1,0 as before. Observe that
these paths use edges of lengths
![]() .
.
![]() ,
obtain the path Pj,0by adding
,
obtain the path Pj,0by adding ![]() to the subscripts of the even vertices of P0,0.
Then the paths
to the subscripts of the even vertices of P0,0.
Then the paths
![]() are obtained by
letting powers of
are obtained by
letting powers of ![]() act on Pj,0. For
act on Pj,0. For
![]() ,
let
,
let
![]() denote the collection of paths
denote the collection of paths
![]() and Bj denote the set of lengths that
and Bj denote the set of lengths that
![]() uses, that is,
uses, that is, ![]()
Observe that
![]() has
b(b'-1) lengths, and thus we must
add b lengths to B to use r/2 lengths. The longest edge used thus
far has length
has
b(b'-1) lengths, and thus we must
add b lengths to B to use r/2 lengths. The longest edge used thus
far has length
![]() or
or
![]() .
Since r < m implies
b < 2d-1a', it follows that
.
Since r < m implies
b < 2d-1a', it follows that
![]() .
Thus, the lengths
.
Thus, the lengths
![]() are distinct.
Furthermore, since (n-2)/2 is an even multiple of
are distinct.
Furthermore, since (n-2)/2 is an even multiple of ![]() ,
we have that
these lengths are all less than (n-2)/2 as well. In
Subcase 2.1, we saw that
,
we have that
these lengths are all less than (n-2)/2 as well. In
Subcase 2.1, we saw that
![]() regardless of the
congruence class of b' modulo 4. Thus B consists of b(b'-1)distinct lengths.
regardless of the
congruence class of b' modulo 4. Thus B consists of b(b'-1)distinct lengths.
![]() is the initial vertex of Pj,i and
is the initial vertex of Pj,i and
![]() is the terminal vertex of Pj,i for
is the terminal vertex of Pj,i for
![]() and
and
![]() .
Now we shall link the paths of
.
Now we shall link the paths of
![]() to
form an m-cycle. We shall use Hamilton cycles in an auxiliary
circulant graph G to do so. Let the vertices of G be labeled
to
form an m-cycle. We shall use Hamilton cycles in an auxiliary
circulant graph G to do so. Let the vertices of G be labeled
![]() .
Suppose we are given a Hamilton cycle
C in G. Arbitrarily orient the cycle C to obtain a Hamilton
directed cycle
.
Suppose we are given a Hamilton cycle
C in G. Arbitrarily orient the cycle C to obtain a Hamilton
directed cycle
![]() .
If there is an arc from vi to
vk in
.
If there is an arc from vi to
vk in
![]() (of length k-i), then insert an edge,
necessarily of length
(of length k-i), then insert an edge,
necessarily of length
![]() ,
from the terminal vertex of
Pj,i to the initial vertex of Pj,k. If we do this for each
arc in
,
from the terminal vertex of
Pj,i to the initial vertex of Pj,k. If we do this for each
arc in
![]() ,
it is easy to see that the paths of
,
it is easy to see that the paths of
![]() are joined together to form an m-cycle. Furthermore,
since the edge from the terminal vertex of Pj,i to the initial
vertex of Pj,k has different length, namely
are joined together to form an m-cycle. Furthermore,
since the edge from the terminal vertex of Pj,i to the initial
vertex of Pj,k has different length, namely
![]() ,
than
the edge from the terminal vertex of Pj,k to the initial vertex of
Pj,i, we can use the reverse orientation
,
than
the edge from the terminal vertex of Pj,k to the initial vertex of
Pj,i, we can use the reverse orientation
![]() of
of
![]() to link the paths in another collection
to link the paths in another collection
![]() ,
,
![]() ,
into an m-cycle. Observe that all the edges used to link
together the paths have lengths congruent to
,
into an m-cycle. Observe that all the edges used to link
together the paths have lengths congruent to
![]() modulo
modulo ![]() and thus none of them have been used in the
construction of the families
and thus none of them have been used in the
construction of the families
![]() .
.
![]() to form
an m-cycle and, in doing so, we use exactly one length in H. However,
if a Hamilton cycle in G uses different lengths for its edges, then
using either orientation to link together paths of some
to form
an m-cycle and, in doing so, we use exactly one length in H. However,
if a Hamilton cycle in G uses different lengths for its edges, then
using either orientation to link together paths of some
![]() ,
results in some edges of lengths congruent to
,
results in some edges of lengths congruent to ![]() modulo
modulo ![]() not
being used. We handle this as follows.
not
being used. We handle this as follows.
![]() is connected. We
decompose it into two Hamilton cycles and orient each of them in the
two possible ways. We then use these four oriented cycles to form four
m-cycles in H. This then uses all the required edges in H of
lengths congruent to
is connected. We
decompose it into two Hamilton cycles and orient each of them in the
two possible ways. We then use these four oriented cycles to form four
m-cycles in H. This then uses all the required edges in H of
lengths congruent to ![]() modulo
modulo ![]() corresponding
to the edges used in the Hamilton cycles. Second, when we are left with
1 or 3 families
corresponding
to the edges used in the Hamilton cycles. Second, when we are left with
1 or 3 families
![]() to link together, we use one or two
Hamilton cycles from G with edges of the same length to complete the
linking process.
to link together, we use one or two
Hamilton cycles from G with edges of the same length to complete the
linking process.
![]() to
link together. If b=1, then let
to
link together. If b=1, then let
![]() so that Gis a (2da')-cycle. In this case, the length
so that Gis a (2da')-cycle. In this case, the length ![]() is used in
H to link
is used in
H to link
![]() into an m-cycle. If b=3, then G has at
least eight vertices so that there are at least two lengths s1 and
s2 relatively prime to 2da'. Then each of s1 and s2generates a Hamilton cycle in
into an m-cycle. If b=3, then G has at
least eight vertices so that there are at least two lengths s1 and
s2 relatively prime to 2da'. Then each of s1 and s2generates a Hamilton cycle in
![]() and
thus we can easily link together the three families of paths into
m-cycles. In this case, the lengths
and
thus we can easily link together the three families of paths into
m-cycles. In this case, the lengths
![]() ,
and
,
and
![]() are used in H to link
are used in H to link
![]() into m-cycles.
into m-cycles.
![]() can be used to link
can be used to link
![]() into an m-
cycle using the length
into an m-
cycle using the length ![]() in H. Next take q successive
pairs
in H. Next take q successive
pairs
![]() ,
all of which generate
connected circulants, to obtain two Hamilton cycles in
,
all of which generate
connected circulants, to obtain two Hamilton cycles in
![]() ,
for
,
for
![]() ,
to link together four
families at a time. Then the lengths
,
to link together four
families at a time. Then the lengths
![]() are used in H. If
b = 4q + 3, then find a second integer
are used in H. If
b = 4q + 3, then find a second integer
![]() relatively prime to 2da' to handle the two extra
families, and the lengths
relatively prime to 2da' to handle the two extra
families, and the lengths
![]() and
and
![]() are used in H.
are used in H.
![]() act on each m-cycle C according to
act on each m-cycle C according to
![]() resulting in a decomposition of
resulting in a decomposition of
![]() into m-cycles. This completes the proof of Theorem 1.1.
into m-cycles. This completes the proof of Theorem 1.1.
Brian &
2000-01-20