

For many real-world processes, like financial market prices, molecular motion and weather patterns, seemingly random fluctuations are intrinsic to their observed behaviour. Understanding the uncertainty in such systems requires a knowledge of the probabilities by which they are ruled, and the statistics by which we can measure them. This plan for this course is to introduce the basic mathematical tools for quantifying the probabilities and statistics of random systems, and to apply these ideas to models with uncertainty. Computational approaches to random simulation and parameter estimation will play an prominent role in the lectures and assignments.
The first part of the term will be an introduction to the mathematics of probability, and the statistics of randomness. The second part of the term will focus on specific problems, and their analysis using probabilistic and statistical methodologies. Assignments will be problem-based, and also require some use of the Matlab computing environment. Possible special topics are: queueing theory, stochastic differential equations, and data assimilation.

 probability in the news (link)
probability in the news (link) probability of precipitation map (link) (pdf)
probability of precipitation map (link) (pdf) probability of precipitation info (link)
probability of precipitation info (link) dna forensics (link)
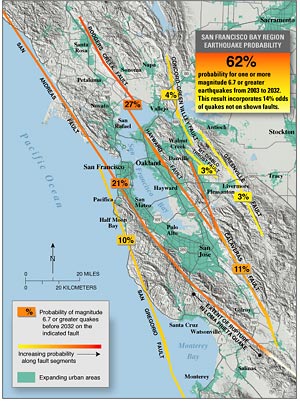
dna forensics (link) earthquake prediction map (link) (pdf)
earthquake prediction map (link) (pdf) radioactive half-life (link)
radioactive half-life (link)
 registration info & instructor's permission, 1:30-4:00pm
registration info & instructor's permission, 1:30-4:00pm please bring unofficial transcript
please bring unofficial transcript syllabus (pdf)
syllabus (pdf) student info sheet (pdf)
student info sheet (pdf) guidelines for reports (pdf)
guidelines for reports (pdf) homework #00 (pdf)
homework #00 (pdf) dice rolling simulation (w01dice.m), type w01dice at the matlab prompt
dice rolling simulation (w01dice.m), type w01dice at the matlab prompt important computing info (text)
important computing info (text)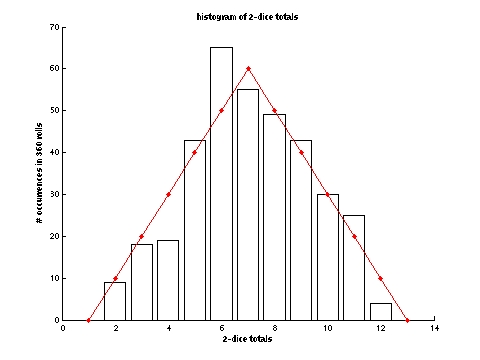
 fall schedule
fall schedule  monday 15:30-17:20, AQ4150
monday 15:30-17:20, AQ4150  wednesday 16:30-17:20, AQ4130
wednesday 16:30-17:20, AQ4130  course abstract (pdf abstract)
course abstract (pdf abstract)

 dice info (link)
dice info (link) matlab intro manual (pdf)
matlab intro manual (pdf)  matlab web info (link)
matlab web info (link)  maple web info (link)
maple web info (link)
