2. Fluid-Structure Interaction and the Immersed Boundary Method

Applying the immersed boundary method to simulate the interaction of an elastic, deformable interface with an incompressible fluid flow. My approach to studying complex fluid-structure interaction problems is two-fold:

• Using analytical techniques to investigate the stability and dynamics of solutions to the immersed boundary equations.
• Applying these analytical insights to better understand the behaviour of numerical schemes and to help design new and more efficient algorithms.

1. Analytical studies of immersed boundaries: I have applied techniques from linear stability analysis and asymptotics to study the stability of solutions to the IB equations. This information is extremely useful since no exact solutions are known, and it also provides insight into the behaviour of commonly used numerical approaches. This work formed the bulk of my PhD thesis and was also published in a number of journal articles [J6], [J2]. I have also investigated the phenomenon of parametric resonance in the context of parametrically-forced immersed boundaries [J11], such as one might see in the heart [J32] or inner ear [J28].

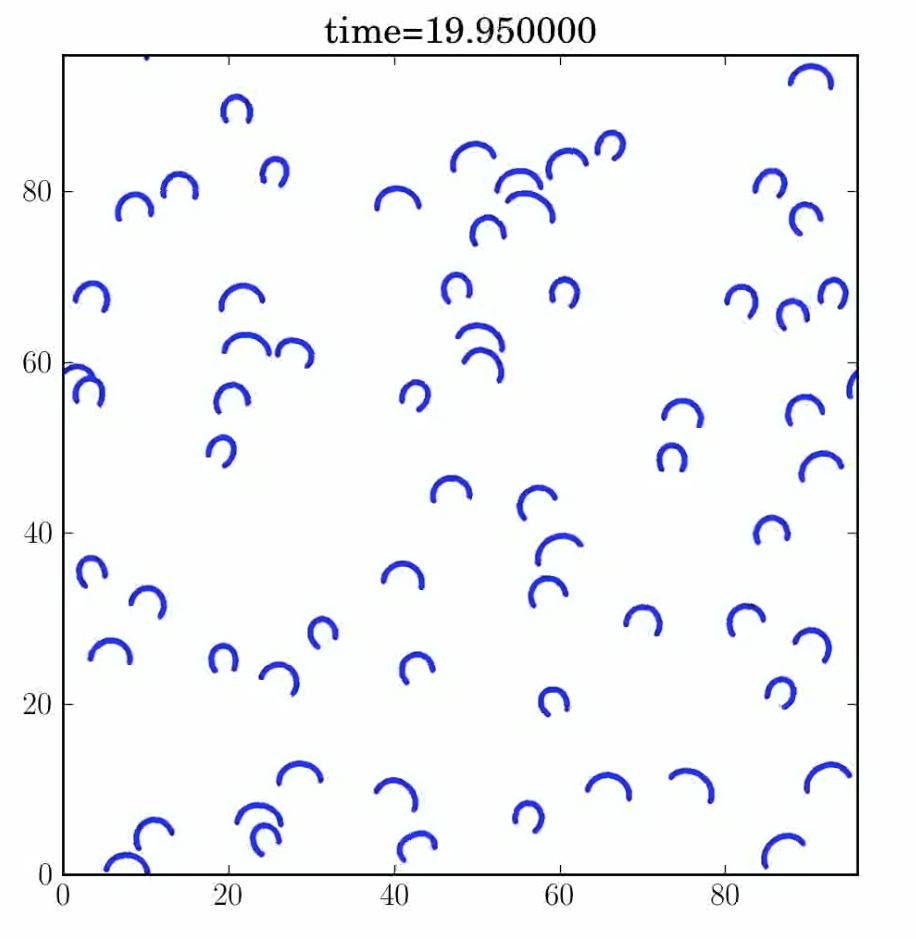
2. Particle suspensions: I have used the immersed boundary method to simulate the rotational dynamics of a single flexible fibre suspended within a planar shear flow. Extensive computations in 2D and 3D [J5], [C5], [J27], show close correspondence with both experimental results and (approximate) analytical solutions. I have also studied sedimentation of rigid circular particles in 2D [J26]. My interest in these problems is partially motivated by the study wood pulp fibres in the papermaking industry.

   2D single-fiber orbits		3D semi-dilute suspensions

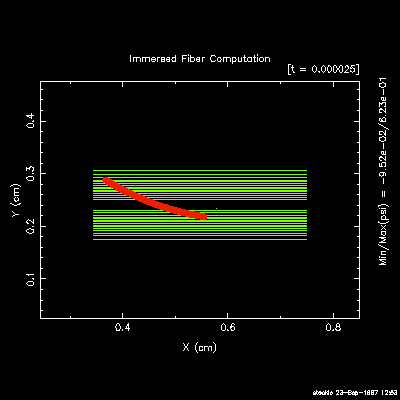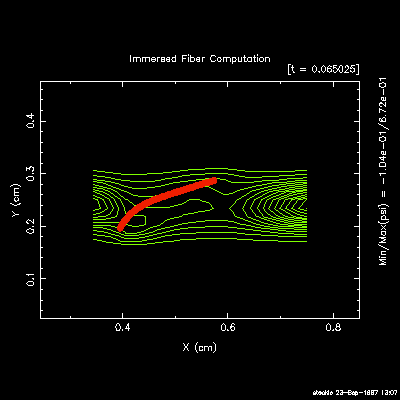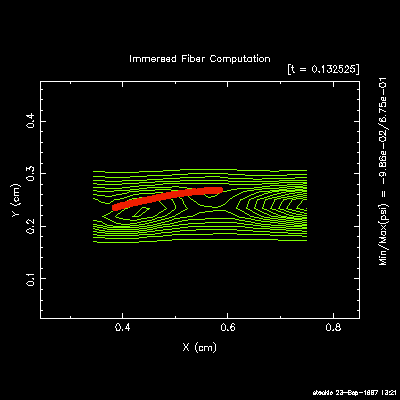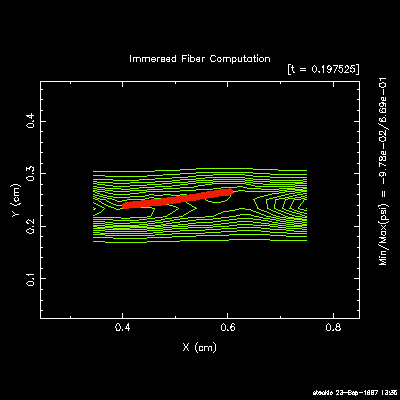3. Membrane transport in porous vesicles: Vesicles are fluid-filled membranes that transport nutrients and other substances within cells through a selectively permeable membrane. To deal with the case where vesicles undergo large deformations and changes in volume, I have extended the IB method to handle porous immersed boundaries and developed a cute approximate analytical solution to go along with it [J14].

4. Biofilm growth and deformation.

5. Swimming dynamics of marine organisms: The IB method has had a long history of simulating the swimming motions of marine worms, flagellated cells, spirochetes, leeches, and other similar organisms. I have a particular interest in the study of squid and jellyfish, whose muscle has a fiber architecture that lends itself ideally to an immersed boundary description. This is ongoing work . . .
   

   2D IB simulation (with MatIB)		Chrysaora fuscescens