4. Scientific Computation

A major component of all the research projects I am involved in is the development of accurate and efficient numerical methods for systems of nonlinear (primarily parabolic) PDEs. I work mostly with finite volume schemes which have been applied in the context of problems in flow in porous media and pollutant transport. Some other examples of related methods I have studied are:

1. High resolution Godunov-type methods for hyperbolic PDEs: in which an approximate analytical solution called a Riemann solver is incorporated into a finite volume scheme to improve the treatment of discontinuities. I have applied these methods in the study of a variety of problems, including:

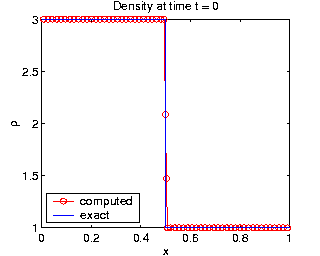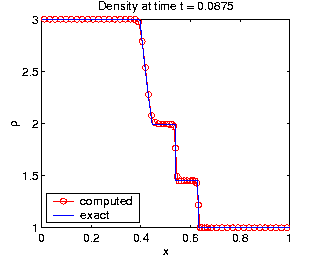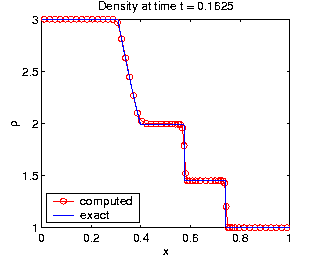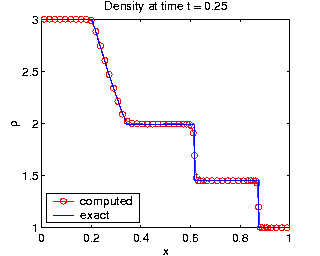
   Density from the Euler equations on a moving grid.

   • a hyperbolic conservation law models for traffic flow with a discontinuous flux [J22].
   • multi-class traffic or pedestrian flow [M1].
   • atmospheric transport in 3D [J37].
   • gas dynamics governed by the Euler equations in 1D [J7], [J1].
   I have made extensive use of CLAWPACK in this work, which is a general and robust publicly-available code for solving hyperbolic conservation laws.

2. Moving mesh methods: in which the mesh points evolve according to a parabolic moving mesh PDE that concentrates points in regions where the solution values or gradients are large. Examples include:
   • Euler equations of gas dynamics [J7] -- more information here.
   • blow-up in parabolic equations with large source terms [J13].
   • resolving wetting fronts in nonlinear diffusion equations.